A rod of length l and negligible mass is suspended at its two ends by two wires of steel (wire A) and aluminium (wire B) of equal lengths (Fig. 9.4). The cross-sectional areas of wires A and B are 1.0 mm2 and 2.0 mm2, respectively. YAl=70
and Ysteel= 200
(a) Mass m should be suspended close to wire A to have equal stresses in both the wires
(b) Mass m should be suspended close to B to have equal stresses in both the wires
(c) Mass m should be suspended at the middle of the wires to have equal stresses in both the wires
(d) Mass m should be suspended close to wire A to have equal strain in both wires
A rod of length l and negligible mass is suspended at its two ends by two wires of steel (wire A) and aluminium (wire B) of equal lengths (Fig. 9.4). The cross-sectional areas of wires A and B are 1.0 mm2 and 2.0 mm2, respectively. YAl=70 and Ysteel= 200
(a) Mass m should be suspended close to wire A to have equal stresses in both the wires
(b) Mass m should be suspended close to B to have equal stresses in both the wires
(c) Mass m should be suspended at the middle of the wires to have equal stresses in both the wires
(d) Mass m should be suspended close to wire A to have equal strain in both wires
-
1 Answer
-
This is a multiple choice answer as classified in NCERT Exemplar
(b), (d) Let mass m is placed at x from the end B respectively.
TA and TB be the tensions in wire A and wire B respectively.
For the rotational equilibrium of the system,
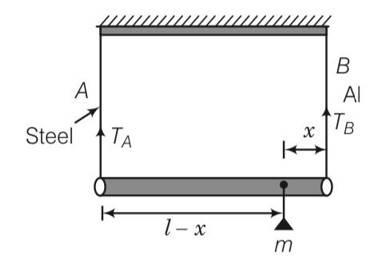
TBx-TA(l-x)=0
=
Stress in wire A = SA=
Stress in wire B = SB= where a are the area of wire
We know that aB=2aA
Now for equal stress
SA=SB
So
So x =l/3 and l-x= 2l/3
Hence mass m should placed to B.
For equal strain
StrainA= StrainB
After solving we get x= x= 10l/17
l-x=l=10l/17=7l/17
Similar Questions for you
If is Poisson's ratio,
Y = 3K (1 - 2 ) ……… (1)
and Y = 2 ……… (2)
With the help of equations (1) and (2), we can write
dm = (m/L)dx
∴ T = (mω²/2L) (L² - x²)
∴ ΔL = ∫? (mω²/2Lπr²Y) (L² - x²)dx
= ΔL = mω²L²/3πr²Y
Initially S? L = 2m
S? L = √2² + (3/2)²
S? L = 5/2 = 2.5 m
? x = S? L - S? L = 0.5 m
So since λ = 1 m. ∴? x = λ/2
So white listener moves away from S? Then? x (= S? L − S? L) increases and hence, at? x = λ first maxima will appear.? x = λ = S? L − S? L.
1 = d - 2 ⇒ d = 3 m.
Loss in elastic potential energy = Gain in KE
½ (YA/L)x² = ½mv²
0.5 * (0.5*10? * 10? / 0.1) * (0.04)² = 20*10? ³ v²
0.5 * (5*10²) * 1.6*10? ³ = 20*10? ³ v²
0.4 = 20*10? ³ v²
v² = 20 => v = √20 ≈ 4.47 m/s
(Re-checking calculations)
0.5 * ( (0.5e9 * 1e-6) / 0.1) * (0.04)^2 = 0.5 * (5e2) * 1.6e-3 = 4.
0.5 * 20e-3 * v^2 = 10e-3 v^2
4 = 10e-3 v^2
v^2 = 400 => v = 20 m/s
As we know that
If length and diameter both are doubled
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers
