A stone of mass m is tied to an elastic string of negligible mass and spring constant k. The unstretched length of the string is L and has negligible mass. The other end of the string is fixed to a nail at a point P. Initially the stone is at the same level as the point P. The stone is dropped vertically from point P.
(a) Find the distance y from the top when the mass comes to rest for an instant, for the first time.
(b) What is the maximum velocity attained by the stone in this drop?
(c) What shall be the nature of the motion after the stone has reached its lowest point?
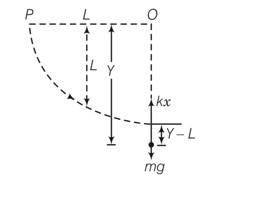
A stone of mass m is tied to an elastic string of negligible mass and spring constant k. The unstretched length of the string is L and has negligible mass. The other end of the string is fixed to a nail at a point P. Initially the stone is at the same level as the point P. The stone is dropped vertically from point P.
(a) Find the distance y from the top when the mass comes to rest for an instant, for the first time.
(b) What is the maximum velocity attained by the stone in this drop?
(c) What shall be the nature of the motion after the stone has reached its lowest point?

-
1 Answer
-
This is a long answer type question as classified in NCERT Exemplar
Till the stone drops through a length L it will be in free fall. After that the elasticity of the spring will force it to a SHM. Let the stone come to rest instantaneously at y.
The loss in PE of the stone is the PE stored in the stretched string .
Mgy=1/2 k(y-L)2
Mgy =
=
Y=
b)in SHM the maximum velocity is attained when the body passes through the equilibrium position i.e when instantaneous acceleration is zero. That is mg-kx=0
so mg=kx
from the conservation of energy
mg=kx
x=mg/k
v2=2gL+mg2/K
v= (2gL+mg2/K)1/2
c)when stone is at lowest position i.e at instantaneo
...more
Similar Questions for you
If is Poisson's ratio,
Y = 3K (1 - 2 ) ……… (1)
and Y = 2 ……… (2)
With the help of equations (1) and (2), we can write
dm = (m/L)dx
∴ T = (mω²/2L) (L² - x²)
∴ ΔL = ∫? (mω²/2Lπr²Y) (L² - x²)dx
= ΔL = mω²L²/3πr²Y
Initially S? L = 2m
S? L = √2² + (3/2)²
S? L = 5/2 = 2.5 m
? x = S? L - S? L = 0.5 m
So since λ = 1 m. ∴? x = λ/2
So white listener moves away from S? Then? x (= S? L − S? L) increases and hence, at? x = λ first maxima will appear.? x = λ = S? L − S? L.
1 = d - 2 ⇒ d = 3 m.
Loss in elastic potential energy = Gain in KE
½ (YA/L)x² = ½mv²
0.5 * (0.5*10? * 10? / 0.1) * (0.04)² = 20*10? ³ v²
0.5 * (5*10²) * 1.6*10? ³ = 20*10? ³ v²
0.4 = 20*10? ³ v²
v² = 20 => v = √20 ≈ 4.47 m/s
(Re-checking calculations)
0.5 * ( (0.5e9 * 1e-6) / 0.1) * (0.04)^2 = 0.5 * (5e2) * 1.6e-3 = 4.
0.5 * 20e-3 * v^2 = 10e-3 v^2
4 = 10e-3 v^2
v^2 = 400 => v = 20 m/s
As we know that
If length and diameter both are doubled
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers
