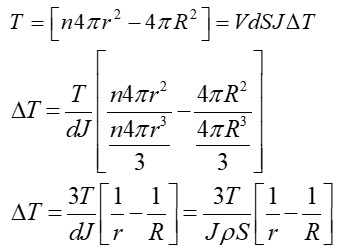A water drop of radius 1cm is broken into 729 equal droplets. If surface tension of water is 75 dyne/cm, then the gain in surface energy upto first decimal place will be:

(Given p = 3.14)

Option 1 - 8.5 × 10-4 J

Option 2 - 8.2 × 10-4 J

Option 3 - 7.5 × 10-4 J

Option 4 - 5.3 × 10-4 J

10 Views|Posted 6 months ago

Asked by Shiksha User

1 Answer

Sort by:

Answered by

Payal Gupta | Contributor-Level 10

6 months ago

Correct Option - 3

Detailed Solution:

$\frac{4}{3} π R^{3} = 729 \frac{4}{3} π r^{3}$

R³= 729r³

$R = (729) \frac{1}{3} (r) (\frac{1}{3})$

R = 9r

$Δ u = T (4 π r^{2}) * 729 - T * 4 π R^{2}$

$= T * 4 π * 8 R^{2}$

$\begin{array}{l} = 75.39 * 1 0^{- 5} J \\ Δ u = 7.5 * 1 0^{- 4} J \end{array}$

Upvote

Similar Questions for you

n droplets of water each of radius r coalesce to form a big drop of radius R. If the energy released during coalescence goes into heating the drop, then the rise in temperature will be (take T as surface tension of water and J as mechanical equivalent of heat)

Raj Pandey

$R = n^{1 / 3} r$

$E = T . Δ A = ms Δ T J$

A water drop of diameter 2 cm is broken into 64 equal droplets. The surface tension of water is 0.075N/m. In this process the gain in surface energy will be:

Raj Pandey

Gain in surface energy, $Δ U = T Δ A$

from volume centenary, $\frac{4}{3} π R^{3} = 64 \times \frac{4}{3} π r^{3}$

$\Rightarrow r = \frac{R}{4}$

Initial surface area, Ai = 4pR²

final surface area, $A_{f} = 64 \times 4 π r^{2}$

$∴ Δ U = 12 π R^{2} . T = 0.075 \times 12 \times 3.14 \times 1 0^{- 4} = 2.8 \times 1 0^{- 4} J$

If temperature of a liquid is increased, choose the correct option regarding change in its surface tension and viscosity.


Vishal Baghel

Fact. Due to decrease in intermolecular forces

When two soap bubbles of radii a and b (b > a) coalesce, the radius of curvature of common surface is:



Vishal Baghel

P? - P? = 4T/a

P? - P? = 4T/b

P? - P? = 4T (1/a - 1/b)

Also, P? - P? = 4T/r

4T/r = 4T (1/a - 1/b)

1/r = (b-a)/ab

r = ab / (b-a)

A large number of water drops, each of radius r, combine to have a drop of radius R. If the surface tension is T and mechanical equivalent of heat is J, the rise in heat energy per unit volume will be

Payal Gupta

From volume conservation

$n \times \frac{4}{3} π r^{3} = \frac{4}{3} π R^{3} \Rightarrow R^{3} = n r^{3} . . . . . . . . . (1)$

Decrease in surface area = $n \times 4 π r^{2} - 4 π R^{2}$

$(Δ A) = 4 π [n r^{2} - R^{2}] = 4 π [\frac{n \times r^{3}}{r} - R^{2}] = 4 π [\frac{R^{3}}{r} - R^{2}] = 4 π R^{3} [\frac{1}{r} - \frac{1}{R}]$

Energy released (W) = $T \times Δ A = 4 π R^{3} T [\frac{1}{r} - \frac{1}{R}]$

Heat produced (Q) = $\frac{W}{J} = \frac{4 π T R^{3}}{J} [\frac{1}{r} - \frac{1}{R}]$

$N o w, Q = m s Δ θ$

$\Rightarrow \frac{4 π R^{3} T}{J} [\frac{1}{r} - \frac{1}{R}] = (\frac{4}{3} π R^{3}) \times | x | \times Δ θ = \frac{3 T}{J} [\frac{1}{r} - \frac{1}{R}]$

Taking an Exam? Selecting a College?

Get authentic answers from experts, students and alumni that you won't find anywhere else.

On Shiksha, get access to

66K

Colleges

1.2K

Exams

6.9L

Reviews

1.8M

Answers

Learn more about...

Physics Mechanical Properties of Fluids 2025

View Exam Details

Share Your College Life Experience

Didn't find the answer you were looking for?

Search from Shiksha's 1 lakh+ Topics

Ask Current Students, Alumni & our Experts

Quick Actions

Community GuidelinesUser Points System

QuestionsDiscussionsTags

Have a question related to your career & education?

See what others like you are asking & answering

A water drop of radius 1cm is broken into 729 equal droplets. If surface tension of water is 75 dyne/cm, then the gain in surface energy upto first decimal place will be: (Given p = 3.14)