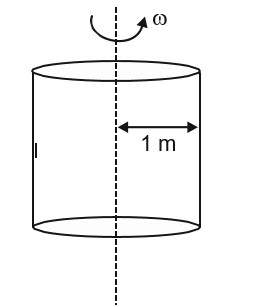
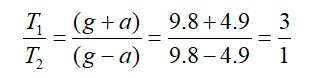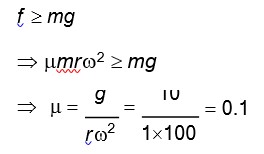An inverted cone is rotating about its vertical axis. A particle is kept on the inner surface of cone and it is at rest relative to the cone at a height of 0.4 m above its vertex. The coefficient of friction between the surface of cone and the particle is 0.6 and the apex angle of cone is 90°. The maximum angular velocity of revolution of the cone can be: (take g = 10/s²)

Option 1 -

12.5rad/s

Option 2 -

10rad/s

Option 3 -

7.5rad/s

Option 4 -

5rad/s

16 Views | Posted 3 weeks ago

Asked by Shiksha User

1 Answer

Answered by

Vishal Baghel | Contributor-Level 10

3 weeks ago

Correct Option - 2

Detailed Solution:

N = (mg/√2) + (mω²h/√2)
(mω²h/√2) = (mg/√2) + f?
(mω²h/√2) = (mg/√2) + μ (mg/√2) + (mω²h/√2)
ω = √ (g/h) (1+μ)/ (1-μ) = 10rad/s

0 Upvotes 0 Downvotes

Similar Questions for you

A mass of 1 kg is suspended by a thread. It is lifted up with an acceleration of 4.9 ms^–2, and then lowered with an acceleration of 4.9 ms^–2 . The ratio of tensions in first case to second cases is (g = 9.8 ms^–2 )

alok kumar singh

T₁ = m (g + a)

T₂ = m (g - a)

Ball released from height 10 m strikes ground and rebounds height 5 m. Find impulse imparted by ground while collision, given mass of ball is 100 g. (Take g = 10 m/s²)

alok kumar singh

$v_{1} = \sqrt[]{2 g 10}$

$v_{2} = \sqrt[]{2 g 5}$

$\vec{l} = Δ \vec{p}$

$l = 0.1 {\sqrt[]{2 g 10} + \sqrt[]{2 g 5}}$

$= 0.1 {10 \sqrt[]{2} + 10}$

$= (\sqrt[]{2} + 1) N s$

A ball is projected from ground with initial momentum p at an angle q. What is the magnitude of net change in linear momentum when it reaches at maximum height of journey?

alok kumar singh

When an elevator is moving downward with a increasing speed, the apparent weight of a body inside elevator

alok kumar singh

Apparent weight = mg – ma

An insect of mass m = 2 g is inside a vertical drum of radius 1 m that is rotating with an angular velocity of 10 rad/s. If the insect does not fall off then the minimum coefficient of friction is