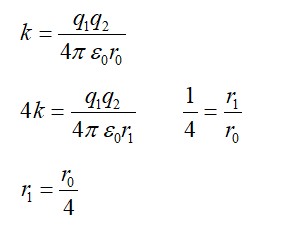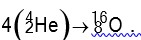Calculate the time interval between 33% decay and 67% decay if half-life of a substance is 20 minutes.

Option 1 - 13 minutes

Option 2 - 60 minutes

Option 3 - 40 minutes

Option 4 - 20 minutes

2 Views|Posted 6 months ago

Asked by Shiksha User

1 Answer

Sort by:

Answered by

Alok Kumar Singh | Contributor-Level 10

6 months ago

Correct Option - 4

Detailed Solution:

N? /N? = e?
For 33% decay, N? /N? = 0.67 ≈ 2/3.
2/3 = e? ⇒ t? = (1/λ)ln (3/2)
For 67% decay, N? /N? = 0.33 ≈ 1/3.
1/3 = e? ⇒ t? = (1/λ)ln (3)
Δt = t? - t? = (1/λ) [ln (3) - ln (3/2)] = (1/λ)ln (2) = T? /? = 20 min

Upvote

Similar Questions for you

The distance of closest approach of an alpha particle fired towards gold nucleus with kinetic energy k is r₀. The distance of closest approach when the alpha particle is fired towards same nucleus with kinetic energy 4k will be

Alok Kumar Singh

Find the mass number of an atom whose radius is half of that of a given atom of mass number 192.

Alok Kumar Singh

$r = R_{0} {(192)}^{\frac{1}{3}}$

$\frac{r}{2} = R_{0} {(m)}^{\frac{1}{3}}$

$m = \frac{192}{8} = 24$

A nuclear fusion reaction is given by If atomic mass of He is 4.0026 amu and that of O is 15.9994 amu then the Q-value of the reaction will be approximately

Alok Kumar Singh

Q = [4 *4.0026 – 15.9994] *931.5 MeV

Q = 10.2 MeV

A radioactive simple is undergoing a decay. At any time t₁, its activity is A and another time t₂, the activity is $\frac{A}{5} .$  What is the average life time for the sample?

Alok Kumar Singh

$A = A_{0} e^{- λ t_{1}}$ [Radio active decay law]

$\frac{A}{5} = A_{0} e^{- λ (t_{2} - t_{1})}$

$\Rightarrow A v e r a g e l i f e = \frac{1}{λ} = \frac{(t_{2} - t_{1})}{l n 5}$

Alok Kumar Singh

$f o r A, t_{\frac{1}{2}} = 4 s e c$

$= m A_{0} e^{-} \frac{0.693}{4} \times 16$

$m_{A} = m_{A 0} e^{- 4 \times 0.693}$ -(1)

for B,

for B, $t_{\frac{1}{2}} = 8 s e c$

$m_{B} = m_{B_{0}} e^{- 2 \times 0.693}$ -(2)

$\frac{m_{A}}{m_{B}} = \frac{m_{A O}}{m_{B O}} \frac{e^{- 4} \times 0.693}{e^{- 2} \times 0.693}$

$\frac{m_{A}}{m_{B}} = \frac{25}{100} = \frac{x}{100} x = 25$

Taking an Exam? Selecting a College?

Get authentic answers from experts, students and alumni that you won't find anywhere else.

On Shiksha, get access to

66K

Colleges

1.2K

Exams

6.9L

Reviews

1.8M

Answers

Learn more about...

Physics Nuclei 2025

View Exam Details

Share Your College Life Experience

Didn't find the answer you were looking for?

Search from Shiksha's 1 lakh+ Topics

Ask Current Students, Alumni & our Experts

Quick Actions

Community GuidelinesUser Points System

QuestionsDiscussionsTags

Have a question related to your career & education?

See what others like you are asking & answering