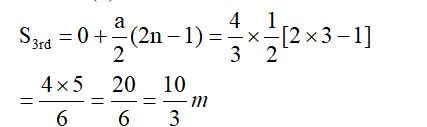Match List – I with List – II :
List – I List – II
(a) h (Planck’s constant) (i)
(b) E (kinetic energy) (ii)
(c) V (electric potential) (iii)
(d) P (linear momentum) (iv)
Choose the correct answer from the options given below:
Match List – I with List – II :
List – I List – II
(a) h (Planck’s constant) (i)
(b) E (kinetic energy) (ii)
(c) V (electric potential) (iii)
(d) P (linear momentum) (iv)
Choose the correct answer from the options given below:
Option 1 -
(a) -> (i), (b) -> (ii), (c) -> (iv), (d) -> (iii)
Option 2 -
(a) -> (iii), (b) ->(ii), (c) -> (iv), (d) -> (i)
Option 3 -
(a) -> (ii), (b) -> (iii), (c) -> (iv), (d) -> (i)
Option 4 -
(a) -> (iii), (b) ->(iv), (c) -> (ii), (d) -> (i)
-
1 Answer
-
Correct Option - 4
Detailed Solution:[h] = ML2T-1
[E] = ML2T-2
[V] = ML2T-2C-1
[P] = MLT-1
Similar Questions for you
Please find the solution below:
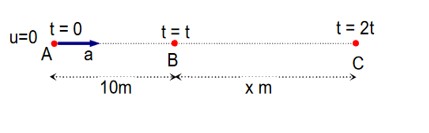
According to question, we can write
10 =
Average speed
(d) Initial velocity
Final velocity
Change in velocity
Momentum gain is along
Force experienced is along
Force experienced is in North-East direction.
h = u²/2g, u = √2gh
Now, S = h/3
S = ut + ½at²
h/3 = √2ght - ½gt²
t² - 2√ (2h/g)t + 2h/3g = 0
Using quadratic formula for t:
t = ( 2√ (2h/g) ± √ (8h/g) - 4 (2h/3g) / 2
t = √ (2h/g) ± √ (2h/g - 2h/3g) = √ (2h/g) ± √ (4h/3g)
t? /t? = (√ (2h/g) - √ (4h/3g) / (√ (2h/g) + √ (4h/3g)
t? /t? = (√2 - √ (4/3) / (√2 + √ (4/3) = (√6 - 2)/ (√6 + 2)
(Note: There is a calculation error in the provided solution. Re-evaluating the physics.)
h/3 = (√2gh)t - ½gt²
(g/2)t² - (&
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers