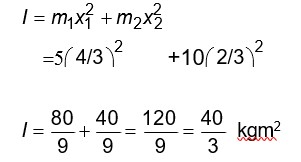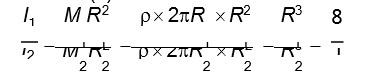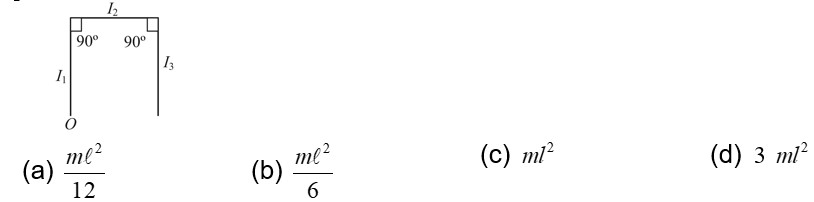The figure shows two solid discs with radius R and r respectively. If mass per unit area is same for both, what is the ratio of MI of bigger disc around axis AB (which is ⊥ to the plane of the disc and passing through its centre) to MI of smaller disc around one of its diameters lying on its plane? Given 'M' is the mass of the larger disc. (MI stands for moment of inertia)
The figure shows two solid discs with radius R and r respectively. If mass per unit area is same for both, what is the ratio of MI of bigger disc around axis AB (which is ⊥ to the plane of the disc and passing through its centre) to MI of smaller disc around one of its diameters lying on its plane? Given 'M' is the mass of the larger disc. (MI stands for moment of inertia)
I? / I? = (MR²/2) / (mr²/4)
[ M = σπR², m = σπr² ]
= 2 (M/m) (R²/r²)
= 2 (σπR²/σπr²) (R²/r²)
= 2 (R²/r²)² = 2R? /r?
Similar Questions for you
= 3.15 kg m2
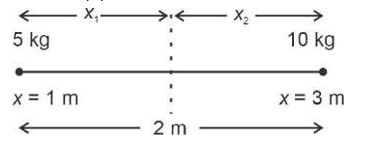
Distance of CM from 5 kg = 10*2/15 = 4/3m
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else.
On Shiksha, get access to
Learn more about...

Physics System of Particles and Rotational Motion 2025
View Exam DetailsMost viewed information
SummaryDidn't find the answer you were looking for?
Search from Shiksha's 1 lakh+ Topics
Ask Current Students, Alumni & our Experts
Have a question related to your career & education?
See what others like you are asking & answering