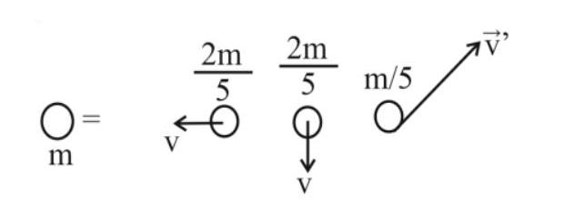
The torque of a force about the origin is . If the force acts on a particle whose position vector is then the value of will be
The torque of a force about the origin is . If the force acts on a particle whose position vector is then the value of will be
Option 1 - <p><span class="mathml" contenteditable="false"> <math> <mrow> <mn>1</mn> <mn>1</mn> <mover accent="true"> <mi>i</mi> <mo>^</mo> </mover> <mo>+</mo> <mn>1</mn> <mn>9</mn> <mover accent="true"> <mi>j</mi> <mo>^</mo> </mover> <mo>−</mo> <mn>4</mn> <mover accent="true"> <mi>k</mi> <mo>^</mo> </mover> </mrow> </math> </span></p>
Option 2 - <p><span class="mathml" contenteditable="false"> <math> <mrow> <mo>−</mo> <mn>1</mn> <mn>1</mn> <mover accent="true"> <mi>i</mi> <mo>^</mo> </mover> <mo>+</mo> <mn>9</mn> <mover accent="true"> <mi>j</mi> <mo>^</mo> </mover> <mo>−</mo> <mn>1</mn> <mn>6</mn> <mover accent="true"> <mi>k</mi> <mo>^</mo> </mover> </mrow> </math> </span></p>
Option 3 - <p><span class="mathml" contenteditable="false"> <math> <mrow> <mo>−</mo> <mn>1</mn> <mn>7</mn> <mover accent="true"> <mi>i</mi> <mo>^</mo> </mover> <mo>+</mo> <mn>1</mn> <mn>9</mn> <mover accent="true"> <mi>j</mi> <mo>^</mo> </mover> <mo>−</mo> <mn>4</mn> <mover accent="true"> <mi>k</mi> <mo>^</mo> </mover> </mrow> </math> </span></p>
Option 4 - <p><span class="mathml" contenteditable="false"> <math> <mrow> <mn>1</mn> <mn>7</mn> <mover accent="true"> <mi>i</mi> <mo>^</mo> </mover> <mo>+</mo> <mn>9</mn> <mover accent="true"> <mi>j</mi> <mo>^</mo> </mover> <mo>+</mo> <mn>1</mn> <mn>6</mn> <mover accent="true"> <mi>k</mi> <mo>^</mo> </mover> </mrow> </math> </span></p>
5 Views|Posted 7 months ago
Asked by Shiksha User
1 Answer
P
Answered by
7 months ago
Correct Option - 3
Detailed Solution:
Similar Questions for you
Use formula for M.I.
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else.
On Shiksha, get access to
66K
Colleges
|
1.2K
Exams
|
6.9L
Reviews
|
1.8M
Answers
Didn't find the answer you were looking for?
Search from Shiksha's 1 lakh+ Topics
or
Ask Current Students, Alumni & our Experts
Have a question related to your career & education?
or
See what others like you are asking & answering