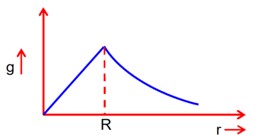
The variation of acceleration due to gravity (g) with distance (r) from the centre of the earth is correctly represented by: (Given R = radius of earth)

Option 1 -

Image 1

Option 2 -

Image 2

Option 3 -

Image 3

Option 4 -

Image 4

4 Views | Posted 3 months ago

Asked by Shiksha User

- Report Abuse

The question is closed for answering

1 Answer

Answered by

Payal Gupta | Contributor-Level 10

3 months ago

Correct Option - 1

Detailed Solution:

$g \propto r 0 \leq r \leq R$

$g \propto \frac{1}{r^{2}} r > R$

0 Upvotes 0 Downvotes

Similar Questions for you

Two 10cm log, straight wires, each carrying a current of 5A are kept parallel to each other. If each wire experienced a force of 10^-5N, then separation between the wires is__________cm.

Vishal Baghel

$F = \frac{μ_{0} \times 2}{4 π} \frac{i_{1} i_{2}}{d} l$

$1 0^{- 5} = \frac{1 0^{- 7} \times 2 \times 5 \times 5}{d} = \frac{10}{100}$

$d = 5 \times 1 0^{- 2} m$

d = 5 cm

The positive feedback is required by an amplifier to act an oscillator. The feedback here means:

Vishal Baghel

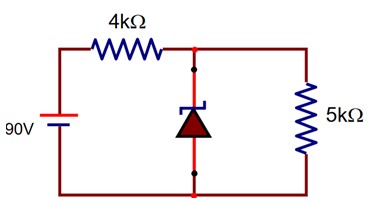
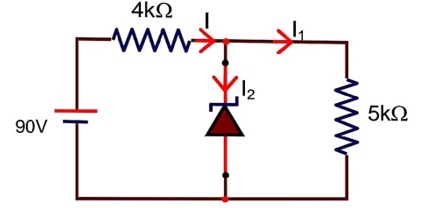
A portion of the output power is returned back to the input.

A transistor is used in an amplifier circuit in common emitter mode. If the best current changes by 100 $μ A,$ it brings a change of 10 mA is collector current. If the load resistance is 2 $k Ω$ and input resistance is 1 $k Ω,$ the value of power gain is x × 10⁴. The value of x is_____________.

alok kumar singh

Power gain = ${(\frac{Δ i_{c}}{Δ i_{b}})}^{2} \times \frac{R_{0}}{R_{i}}$

= ${(\frac{10 \times 1 0^{- 3}}{100 \times 1 0^{- 6}})}^{2} \times \frac{2}{1}$

= 2 × 104 = x × 104

= 2

The typical transfer characteristics of a transistor in CE configuration is shown in figure. A load resistor of $2 k Ω$ is connected in the collector branch of the circuit used. The input resistance of the transistor is $0.50 k Ω .$ The voltage gain of the transistor is________.