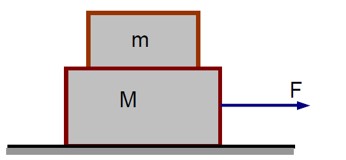
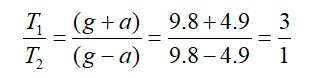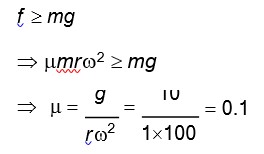Two blocks (m = 0.5kg and M = 4.5kg) are arranged on a horizontal frictionless table as shown in figure. The coefficient of static friction between the two blocks is 3/7. Then the maximum horizontal force that can be applied on the block so that blocks move together is ---------N. (Round off to the Nearest Integer) [ Take g as 9.8 ms^-2]

4 Views | Posted a month ago

Asked by Shiksha User

1 Answer

Answered by

Vishal Baghel | Contributor-Level 10

a month ago

For the combined system of mass M and m, the acceleration under an applied force F is:
a = F / (M + m)

The static friction force (f_s) on the top block (m) provides its acceleration:
f_s = MA = m * [F / (M + m)] = mF / (M + m)

For the top block not to slip, the required static friction must be less than or equal to the maximum possible static friction (μmg):
f_s ≤ μmg
mF / (M + m) ≤ μmg
F ≤ μ (M + m)g

Using the values implied in the solution:
F ≤ 21 N

0 Upvotes 0 Downvotes

Similar Questions for you

A mass of 1 kg is suspended by a thread. It is lifted up with an acceleration of 4.9 ms^–2, and then lowered with an acceleration of 4.9 ms^–2 . The ratio of tensions in first case to second cases is (g = 9.8 ms^–2 )

alok kumar singh

T₁ = m (g + a)

T₂ = m (g - a)

Ball released from height 10 m strikes ground and rebounds height 5 m. Find impulse imparted by ground while collision, given mass of ball is 100 g. (Take g = 10 m/s²)

alok kumar singh

$v_{1} = \sqrt[]{2 g 10}$

$v_{2} = \sqrt[]{2 g 5}$

$\vec{l} = Δ \vec{p}$

$l = 0.1 {\sqrt[]{2 g 10} + \sqrt[]{2 g 5}}$

$= 0.1 {10 \sqrt[]{2} + 10}$

$= (\sqrt[]{2} + 1) N s$

A ball is projected from ground with initial momentum p at an angle q. What is the magnitude of net change in linear momentum when it reaches at maximum height of journey?

alok kumar singh

When an elevator is moving downward with a increasing speed, the apparent weight of a body inside elevator

alok kumar singh

Apparent weight = mg – ma

An insect of mass m = 2 g is inside a vertical drum of radius 1 m that is rotating with an angular velocity of 10 rad/s. If the insect does not fall off then the minimum coefficient of friction is