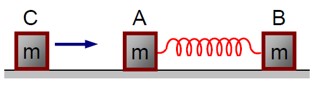
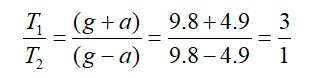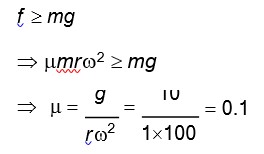Two identical blocks A and B each of mass m resting on the smooth horizontal floor are connected by a light spring of natural L and spring constant K. A third block C of mass m moving with a speed v along the line joining A and B collides with A. The maximum compression in the spring is:

Option 1 -

mv / √K

Option 2 -

mv / √2K

Option 3 -

√(m/2K) * v

Option 4 -

v * √(m/2K)

4 Views | Posted a month ago

Asked by Shiksha User

1 Answer

Answered by

alok kumar singh | Contributor-Level 10

a month ago

Correct Option - 4

Detailed Solution:

For an elastic collision where C comes to rest, and the compression in the spring is maximum, the velocities of A and B are equal (v). Using the conservation of mechanical energy:
(1/2)mv? ² = 2 * (1/2)mv² + (1/2)kx²
This gives the maximum compression x as:
x = v? * √* (m / 2k)*

0 Upvotes 0 Downvotes

Similar Questions for you

A mass of 1 kg is suspended by a thread. It is lifted up with an acceleration of 4.9 ms^–2, and then lowered with an acceleration of 4.9 ms^–2 . The ratio of tensions in first case to second cases is (g = 9.8 ms^–2 )

alok kumar singh

T₁ = m (g + a)

T₂ = m (g - a)

Ball released from height 10 m strikes ground and rebounds height 5 m. Find impulse imparted by ground while collision, given mass of ball is 100 g. (Take g = 10 m/s²)

alok kumar singh

$v_{1} = \sqrt[]{2 g 10}$

$v_{2} = \sqrt[]{2 g 5}$

$\vec{l} = Δ \vec{p}$

$l = 0.1 {\sqrt[]{2 g 10} + \sqrt[]{2 g 5}}$

$= 0.1 {10 \sqrt[]{2} + 10}$

$= (\sqrt[]{2} + 1) N s$

A ball is projected from ground with initial momentum p at an angle q. What is the magnitude of net change in linear momentum when it reaches at maximum height of journey?

alok kumar singh

When an elevator is moving downward with a increasing speed, the apparent weight of a body inside elevator

alok kumar singh

Apparent weight = mg – ma

An insect of mass m = 2 g is inside a vertical drum of radius 1 m that is rotating with an angular velocity of 10 rad/s. If the insect does not fall off then the minimum coefficient of friction is