Ask & Answer Question

Ncert Solutions Maths class 11th Maths Class 11th Straight Lines

2. The base of an equilateral triangle with side 2a lies along the y-axis such that the mid-point of the base is at the origin. Find vertices of the triangle.

44 Views | Posted 4 months ago

Asked by Shiksha User

1 Answer

Answered by

alok kumar singh | Contributor-Level 10

4 months ago

2. Let ABC be the equilateral triangle of side 2a and 0 be the origin. Then

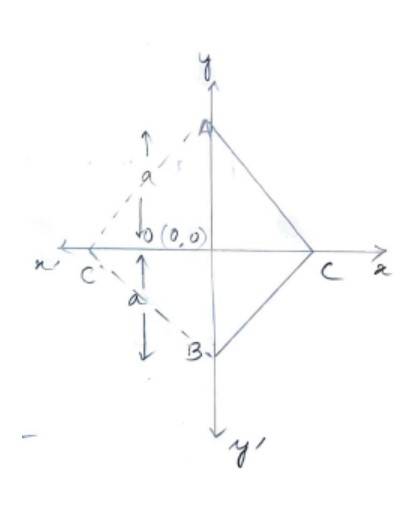
AB = BC = AC = 2a

O is the mid-point of AB we have AO = a

BO = a

We know that A and B lies on y-axis so they have co-ordinate of the form (0, y).

Hence, co-ordinate of A is (0, a) and that of B is (0, –a)

Since OC, bisects AB at right angle, by Pythagoras theorem,

AC²= OA² + OC²

$\Rightarrow {(2 a)}^{2} = {(a)}^{2} +OC^{2}$

$\RightarrowOC^{2} = 4 a^{2} - a^{2}$

And as C we on x-axis it has co-ordinate of the form (x, 0)

0 Upvotes 0 Downvotes

Similar Questions for you

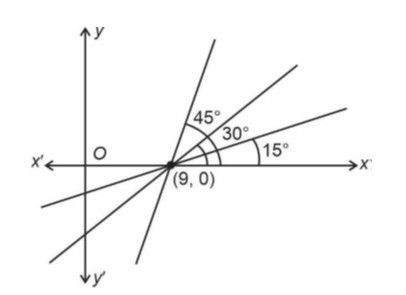
A line passes through (9, 0), making angle 30° with positive direction of x-axis. It is rotated by angle of 15° with respect to (9, 0). Then one of the equation of new line is

alok kumar singh

Eqⁿ : y – 0 = tan45° (x – 9) Þ y = (x – 9)

Option (B) is correct

If two circle x² + y² = 4 and x² + y² – 4lx + 9 = 0 intersect at two distinct points, then find the range of l.

alok kumar singh

|r₁ – r₂| < c₁c₂ < r₁ + r₂

-> $| 2 - \sqrt[]{4 λ^{2} - 9} | < | 2 λ | < 2 + \sqrt[]{4 λ^{2} - 9}$

$| 2 λ | - 2 < \sqrt[]{4 λ^{2} - 9}$

$4 λ^{2} + 4 - 8 | λ | < 4 λ^{2} - 9$

$λ > \frac{13}{8}, λ < - \frac{13}{8}$

$\sqrt[]{4 λ^{2} - 9} > 0$

$λ > \frac{3}{2}, λ < - \frac{3}{2}$

$λ \in (- \infty, - \frac{13}{8}) \cup (\frac{13}{8}, \infty)$

Now,

$| 2 - \sqrt[]{4 λ^{2} - 9} | < | 2 λ |$

$4 + 4 λ^{2} - 9 - 4 \sqrt[]{4 λ^{2} - 9} < 4 λ^{2}$

$4 \sqrt[]{4 λ^{2} - 9} > - 5 \Rightarrow λ \in R$

$λ \in (- \infty, - \frac{13}{8}) \cup (\frac{13}{8}, \infty)$

The line passes through the centre of circle x² + y² – 16x – 4y = 0, it interacts with the positive coordinate axis at A & B. Then find the minimum value of OA + OB, where O is origin.

alok kumar singh

(y – 2) = m (x – 8)

⇒ x-intercept

⇒ $(\frac{- 2}{m} + 8)$

⇒ y-intercept

⇒ (–8m + 2)

⇒ OA + OB = $\frac{- 2}{m^{2}}$ + 8 – 8m + 2

$f' (m) = \frac{2}{m^{2}} - 8 = 0$

-> $m^{2} = \frac{1}{4}$

-> $m = \frac{- 1}{2}$

-> $f (\frac{- 1}{2}) = 18$

->Minimum = 18

The image of the point (3, 5) in the line x – y + 1 = 0, lies on:

Vishal Baghel

Kindly consider the following figure

A man is walking on a straight line. The arithmetic mean of the reciprocals of the intercepts of the line on the coordinate axes is $\frac{1}{4} .$ Three stones A, B and C are placed at the point (1, 1), (2, 2) and (4, 4) respectively. Then which of these stones is / are on the path of the man?

Vishal Baghel

According to question,

$\frac{1}{2} (\frac{1}{a} + \frac{1}{b}) = \frac{1}{4}$

$\frac{1}{a} + \frac{1}{b} = \frac{1}{2} . . . . . . . . (i)$

Equation of required line is $\frac{x}{a} + \frac{y}{b} = 1$ $\frac{}{} \frac{}{}$

Obviously B (2, 2) satisfying condition (i)

Get authentic answers from experts, students and alumni that you won't find anywhere else

On Shiksha, get access to

65k Colleges
1.2k Exams
687k Reviews
1800k Answers

Community GuidelinesUser Points System

QuestionsDiscussionsTags

2. The base of an equilateral triangle with side 2a lies along the y-axis such that the mid-point of the base is at the origin. Find vertices of the triangle.

1 Answer

Similar Questions for you

Learn more about...

Most viewed information

Share Your College Life Experience

Didn't find the answer you were looking for?

Need guidance on career and education? Ask our experts

Your Question