42. x + y ≤ 6, x + y ≥ 4
42. x + y ≤ 6, x + y ≥ 4
-
1 Answer
-
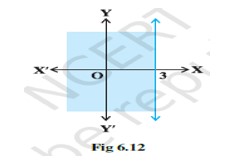
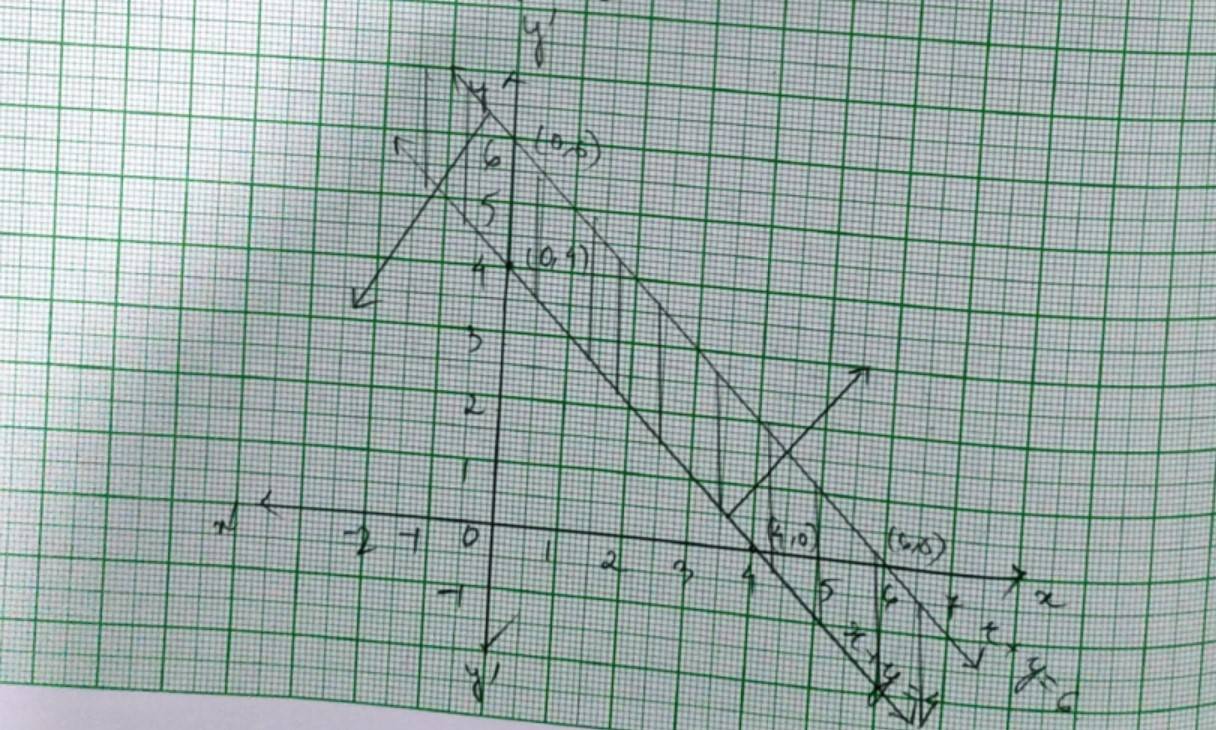
42. The given system of inequality is
x+y≤ 6 - (1)
x+y≥ 4- (2)
So the corresponding equations are
x+y=6
x
0
6
y
6
0
and x + y = 4
x
4
0
y
0
4
Putting (x, y)= (0,0) in equality (1) and (2),
0+0 ≤ 6 and 0 + 0 ≥ 4
0 ≤ 6 is true. => 0 ≥ 4 is false.
So, solution of plane of inequality (1) includes the origin and inequality (2) does not includes the origin.
? The reqd solution of the given system of inequality is the shaded region.
Similar Questions for you
centre
radius
centre
OA =
r2 =
Let y = mx + c is the common tangent
so equation of common tangents will be
which intersects at Q (3, 0)
Major axis and minor axis of ellipse are 12 and 6. So eccentricity
and length of latus rectum
Hence
This is a Fill in the blanks Type Questions as classified in NCERT Exemplar
This is a True or False Type Questions as classified in NCERT Exemplar
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers