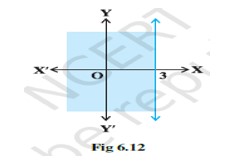
47. 2x + y ≥ 4, x + y ≤ 3, 2x – 3y ≤ 6
47. 2x + y ≥ 4, x + y ≤ 3, 2x – 3y ≤ 6
-
1 Answer
-
47. The given system of inequality is
2x + y ≥ 4- (1)
x + y ≤ 3- (2)
2x – 3y ≤ 6- (3)
The corresponding equation are
2x + y = 4
x
2
0
y
0
4
and x + y = 3
x
0
3
y
3
0
and 2x + 3y = 6
x
3
0
y
0
–2
Putting (x, y)= (0,0) in (1), (2) and (3),
2 × 0+0 ≥ 4
0 ≥ 4 which is false.
and 0+0 ≤ 3 => 0 ≤ 3 which is true.
and 2 × 0 – 3 × 0 ≤ 6 => 0 ≤ 6which is also true.
So, solution of inequality (1) excludes plane with origin while solution of inequality (2) and (3) includes the plane with origin.

Similar Questions for you
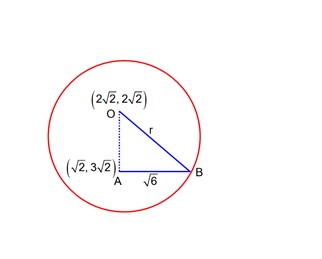
centre
radius
centre
OA =
r2 =
Let y = mx + c is the common tangent
so equation of common tangents will be
which intersects at Q (3, 0)
Major axis and minor axis of ellipse are 12 and 6. So eccentricity
and length of latus rectum
Hence
This is a Fill in the blanks Type Questions as classified in NCERT Exemplar
This is a True or False Type Questions as classified in NCERT Exemplar
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers