72. If sum of the perpendicular distances of a variable point P (x, y) from the lines x + y – 5 = 0 and 3x – 2y +7 = 0 is always 10. Show that P must move on a line.
72. If sum of the perpendicular distances of a variable point P (x, y) from the lines x + y – 5 = 0 and 3x – 2y +7 = 0 is always 10. Show that P must move on a line.
-
1 Answer
-
72. The given eqn of the lines are.
x + y ? 5 = 0 _______ (1)
3x ? 2y + 7 = 0 ______ (2)
Given, sum of perpendicular distance of P (x, y) from the two lines is always 10 .
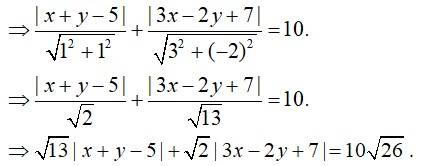
The above eqn can be expressed as a linear combination Ax + By + C = 0 where A, B & C are constants representing a straight line
P (x, y) mover on a line.
Similar Questions for you
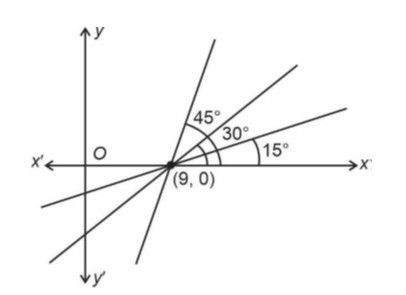
Eqn : y – 0 = tan45° (x – 9) Þ y = (x – 9)
Option (B) is correct
|r1 – r2| < c1c2 < r1 + r2
->
Now,
(y – 2) = m (x – 8)
⇒ x-intercept
⇒
⇒ y-intercept
⇒ (–8m + 2)
⇒ OA + OB =
->
->
->
->Minimum = 18
Kindly consider the following figure
According to question,
Equation of required line is
Obviously B (2, 2) satisfying condition (i)
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers