Let A be the set of all points (α, β) such that the area of triangle formed by the points (5, 6), (3, 2) and (α, β) is 12 square units. Then the least possible length of a line segment joining the origin to a point in A, is :
Let A be the set of all points (α, β) such that the area of triangle formed by the points (5, 6), (3, 2) and (α, β) is 12 square units. Then the least possible length of a line segment joining the origin to a point in A, is :
Option 1 -
Option 2 -
Option 3 -
Option 4 -
-
1 Answer
-
Correct Option - 4
Detailed Solution:Distance of origin
if 2 - = 16
Similar Questions for you
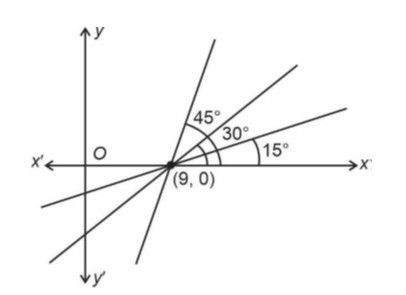
Eqn : y – 0 = tan45° (x – 9) Þ y = (x – 9)
Option (B) is correct
|r1 – r2| < c1c2 < r1 + r2
->
Now,
(y – 2) = m (x – 8)
⇒ x-intercept
⇒
⇒ y-intercept
⇒ (–8m + 2)
⇒ OA + OB =
->
->
->
->Minimum = 18
Kindly consider the following figure
According to question,
Equation of required line is
Obviously B (2, 2) satisfying condition (i)
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers