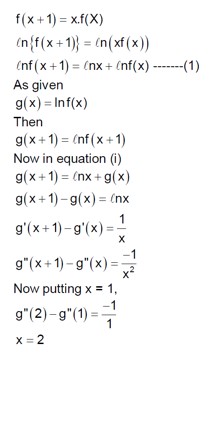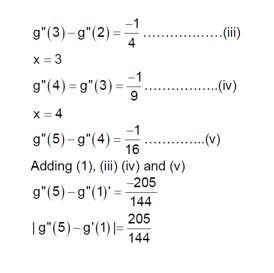Let f:S → S where S = (0,∞) be a twice differentiable function such that f(x+1) = xf(x). If g: S → R be defined as g(x) = logₑf(x), then the value of |g''(5)-g''(1)| is equal to :
Let f:S → S where S = (0,∞) be a twice differentiable function such that f(x+1) = xf(x). If g: S → R be defined as g(x) = logₑf(x), then the value of |g''(5)-g''(1)| is equal to :
Option 1 -
205/144
Option 2 -
197/144
Option 3 -
187/144
Option 4 -
1
-
1 Answer
-
Correct Option - 1
Detailed Solution:
Similar Questions for you
Logarithmic differentiation is used in the following cases:
- Logarithmic differentiation is used with functions that have a variable in both base and exponents. In such a case, standard differentiation rules do not apply directly to such functions. This differentiation converts exponentiation into multiplication.
- Another area where logarithmic differentiation is used is with a function which is the product of a quotient of multiple terms.
- Whenever a function has a complex combination of multiplication, division and exponentiation, logarithmic differentiation is preferred. This differentiation eases the complexity by converting multip
RHL
LHL
Given
If f (x) is continuous for all then it should be continuous at x = 1 & x = -1
At x = -1, L.H.L = R.H.L. Þ 2 = |a + b - 1|
->a + b – 3 = 0 OR a + b + 1 = 0 . (i)
-> a + b + 1 = 0 . (ii)
(i) & (ii), a + b =-1
Given f(x) =
using Leibniz rule then
f’(x) = exf(x) + ex
P = -ex, Q = ex
Solution be y. (I.F.) =
I. f. =
Put x = 0 , in (i) f (0) = 1
Hence f(x) = 2.
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers