Search Colleges, Courses, Exams, Questions and Articles

Ask a query on 8879100846 Ask Login | Sign Up

 

 

› Ask & Answer › Question

Let M be any 3 × 3 matrix with entires from the set {0, 1, 2}. The maximum number of such matrices, for which the sum of diagonal elements MTM is seven is____________.

0 2 Views | Posted a month ago
Asked by Shiksha User

  • 1 Answer

  • A

    Answered by

    alok kumar singh | Contributor-Level 10

    a month ago

    M = [ a 1 a 2 a 3 b 1 b 2 c 3 c 1 c 2 c 3 ]    

    M T M = [ a 1 b 1 c 1 a 2 b 2 c 2 a 3 b 3 c 3 ] [ a 1 a 2 a 3 b 1 b 2 b 3 c 1 c 2 c 3 ]

    T r ( M T M ) = a 1 2 + b 1 2 + c 1 2 + a 2 2 + b 2 2 + c 2 2 + a 3 2 + b 3 2 + c 3 2 = 7           

    all   a i , b i , c i ∈ { 0 , 1 , 2 } f o r     i = 1, 2, 3

    Case 1 7 one’s and two zeroes which can occur in ways

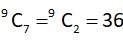
    Case 2 One 2 three 1’s five zeroes =

     

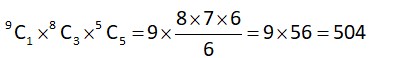
    total such matrices = 504 + 36 = 540

     

Similar Questions for you

If the matrix A = [ 1 0 0 0 2 0 3 0 − 1 ]  satisfies the equation A20 = aA19 + βA = [ 1 0 0 0 4 0 0 0 1 ] for some real numbers a and b, then b - a is equal to…………
A
alok kumar singh

  A 2 = [ 1 0 0 0 2 0 3 0 − 1 ] [ 1 0 0 0 2 0 3 0 − 1 ] = [ 1 0 0 0 2 2 0 0 0 1 ]

A 3 = [ 1 0 0 0 2 2 0 0 0 1 ] [ 1 0 0 0 2 0 3 0 − 1 ] = [ 1 0 0 0 2 3 0 3 0 − 1 ]        

A 4 [ 1 0 0 0 2 3 0 3 0 − 1 ] [ 1 0 0 0 2 0 3 0 − 1 ] = [ 1 0 0 0 2 4 0 0 0 1 ]          

Similarly we get A19 =   = [ 1 0 0 0 2 1 9 0 3 0 − 1 ] & A 2 0 = [ 1 0 0 0 2 2 0 0 0 0 1 ]

=   [ 1 0 0 0 4 0 0 0 1 ]

⇒ 1 + α + β = 1 g i v e s     α + β = 0 . . . . . . . . ( i )        

  2 2 0 + ( 2 1 9 − 2 ) α = 4 f r o m ( i )

⇒ α = 4 − 2 2 0 2 1 9 − 2 = 4 ( 1 − 2 1 8 ) − 2 ( 1 − 2 1 8 ) = − 2          

So, b = 2

Hence b - a = 4

 

Consider the following system of equations:

x + 2y – 3z = a                     

2x + 6y – 11z = b

x – 2y + 7z = c,

where a, b and c are real constants. Then the system of equations:
A
alok kumar singh

Given x + 2y – 3z = a

2x + 6y – 11z = b

x – 2y + 7z = c

Here    Δ = | 1 2 − 3 2 6 − 1 1 1 − 2 7 | = ( 4 2 − 2 2 ) − 2 ( 1 4 + 1 1 ) − 3 ( − 4 − 6 ) = 2 0 − 5 0 + 3 0 = 0                                                                                

For infinite solution 

20a – 8b – 4c = 0 Þ 5a = 2b + c

Let A = { n ∈ N : H . C . F . ( n , 4 5 ) = 1 } and Let B = { 2 k : k ∈ { 1 ,   2 , . . . . . . ,   1 0 0 } } . Then the sum of all the elements of   A ∪ B     i s . . . . . . . . . .  
R
Raj Pandey

Sum of all elements of A ∩ B = 2   [Sum of natural number upto 100 which are neither divisible by 3 nor by 5]

= 2 [ 1 0 0 × 1 0 1 2 − 3 ( 3 3 × 3 4 2 ) − 5 ( 2 0 × 2 1 2 ) + 1 5 ( 6 × 7 2 ) ]

= 10100 – 3366 – 2100 + 630

              = 5264

Let  A = ( 2 − 1 0 2 ) . If B = I − 5 ​ C 1 ( a d j A ) + 5 ​ C 2 ( a d j A ) 2 − . . . 5 ​ C 5 ( a d j A ) 5 ,  then the sum of all elements of the matrix B is
A
alok kumar singh

Kindly go through the solution

B = (I – adjA)5

Let M = [ 0 − α α 0 ] , where a is a non-zero real number an N = ∑ k = 1 4 9 M 2 k . If (I – M2)N = -2I, then the positive integral value of a is…………….
A
alok kumar singh

N = M 2 + M 4 + . . . . . + M 9 8

= ( − α 2     I ) + ( − α 2     I ) 2 + . . . . + ( − α 2     I ) 4 9

= I ( − α 2 + α 4 − α 6 + . . . . − α 9 8 )

N =  − I ( α 2 − α 4 + α 6 . . . . . . . + α 9 8 )

= − I α 2 ( 1 − ( − α 2 ) 4 9 ) 1 − ( − α 2 )

N =  − I   α 2 ( 1 + α 9 8 ) 1 + α 2  

Now  ( I − m 2 ) N = − 2 I

( I + α 2 I ) ( − I α 2 ⋅ ( 1 + α 9 8 ) 1 + α 2 = − 2 I  

-> a100 + a2 = 2

->a = ± 1

Get authentic answers from experts, students and alumni that you won't find anywhere else

Sign Up on Shiksha

On Shiksha, get access to

  • 65k Colleges
  • 1.2k Exams
  • 687k Reviews
  • 1800k Answers

Learn more about...

Share Your College Life Experience

Write a Review

Didn't find the answer you were looking for?

Search from Shiksha's 1 lakh+ Topics

or

Ask Current Students, Alumni & our Experts

Ask Now
Community GuidelinesUser Points System
QuestionsDiscussionsTags
×
×

This website uses Cookies and related technologies for the site to function correctly and securely, improve & personalise your browsing experience, analyse traffic, and support our marketing efforts and serve the Core Purpose. By continuing to browse the site, you agree to Privacy Policy and Cookie Policy.

Need guidance on career and education? Ask our experts

Characters 0/140

The Answer must contain atleast 20 characters.

Add more details

Characters 0/300

The Answer must contain atleast 20 characters.

Keep it short & simple. Type complete word. Avoid abusive language. Next

Your Question

Edit

Add relevant tags to get quick responses. Cancel Post