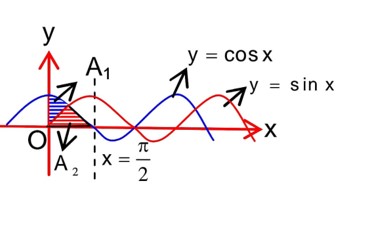
The area of the region, enclosed by the circle x² + y² = 2, which is not common to the region bounded by the parabola y² = x and the straight line y = x, is:
The area of the region, enclosed by the circle x² + y² = 2, which is not common to the region bounded by the parabola y² = x and the straight line y = x, is:
Option 1 -
(1/6)(12π – 1)
Option 2 -
(1/3)(6π – 1)
Option 3 -
(1/6)(12π – 1)
Option 4 -
(1/6)(24π – 1)
-
1 Answer
-
Correct Option - 3
Detailed Solution:Area A = 2π - ∫? ¹ (√x - x) dx is incorrect. The area is likely between two curves.
The calculation shown is:
A = 2π - [2/3 x^ (3/2) - x²/2] from 0 to 1.
A = 2π - (2/3 - 1/2) = 2π - (4/6 - 3/6) = 2π - 1/6 = (12π - 1)/6.
Similar Questions for you
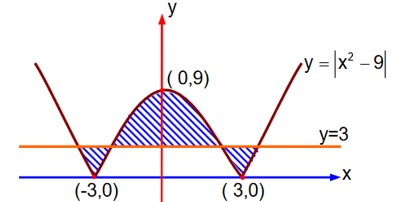
Required area = A
Note : No option in the question paper is correct.
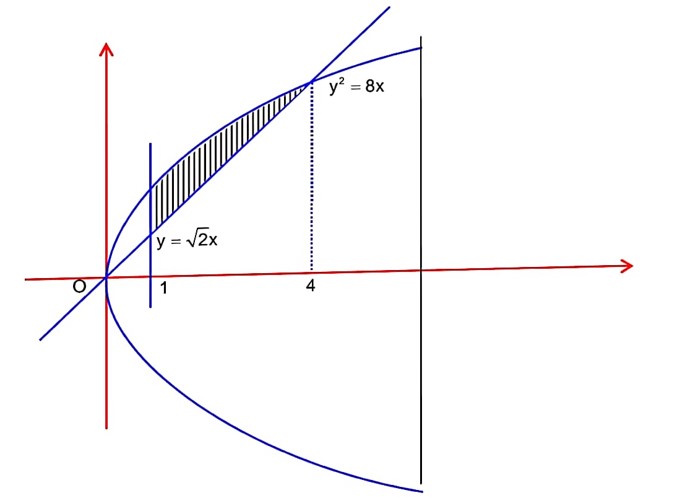
Required area = dx
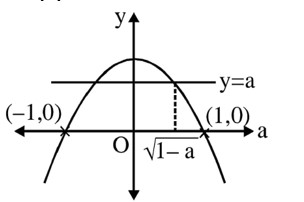
and
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers