The value of lim(n→∞) ([r] + [2r] + ... + [nr]) / n², where r is a non-zero real number and [r] denotes the greatest integer less than or equal to r, is equal to:
The value of lim(n→∞) ([r] + [2r] + ... + [nr]) / n², where r is a non-zero real number and [r] denotes the greatest integer less than or equal to r, is equal to:
Option 1 -
r/2
Option 2 -
2r
Option 3 -
r
Option 4 -
0
-
1 Answer
-
Correct Option - 1
Detailed Solution:Limit (n→∞) [[r] + [2r] + . + [nr]] / n²
We know that x - 1 < [x] ≤ x.
Summing from k=1 to n for [kr]:
Σ(kr - 1) < Σ[kr] ≤ Σ(kr)
rΣk - Σ1 < Σ[kr] ≤ rΣk
r(n(n+1)/2) - n < Σ[kr] ≤ r(n(n+1)/2)Divide by n²:
(r/2)(1 + 1/n) - 1/n < (Σ[kr])/n² ≤ (r/2)(1 + 1/n)As n → ∞, both the left and right sides approach r/2.
By the Squeeze Theorem, the limit is r/2.
Similar Questions for you
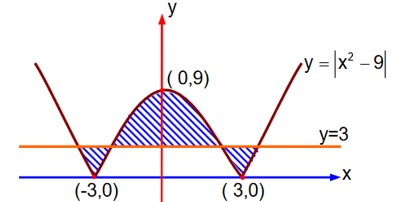
Required area = A
Note : No option in the question paper is correct.
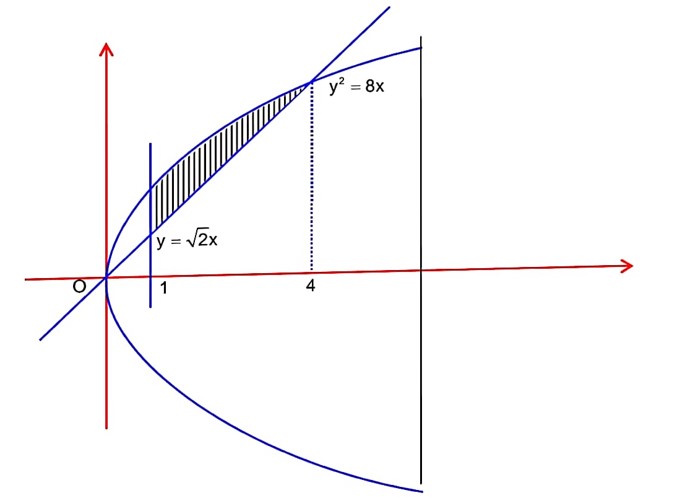
Required area = dx
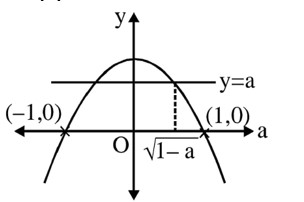
and
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers