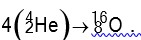13.8 The normal activity of living carbon-containing matter is found to be about 15 decays per minute for every gram of carbon. This activity arises from the small proportion of radioactive ${}_{6}^{14}C$ present with the stable carbon isotope ${}_{6}^{12}C$ . When the organism is dead, its interaction with the atmosphere (which maintains the above equilibrium activity) ceases and its activity begins to drop. From the known half-life (5730 years) of ${}_{6}^{14}C$ , and the measured activity, the age of the specimen can be approximately estimated. This is the principle of ${}_{6}^{14}C$ dating used in archaeology. Suppose a specimen from Mohenjo-Daro gives an activity of 9 decays per minute per gram of carbon. Estimate the approximate age of the Indus-Valley civilization.

3 Views | Posted 5 months ago

Answered by

Payal Gupta | Contributor-Level 10

3 months ago

13.8 Decay rate of living carbon-containing matter, R = 15 decay / min

Half life of ${}_{6}^{14}C$ , $T_{1 / 2}$ = 5730 years

Decay rate of the specimen obtained from the Mohenjo-Daro site, R’ = 9 decays/min

Let N be the number of radioactive atoms present in a normal carbon-containing matter.

Let N’ be the number of radioactive atoms present in the specimen during the Mohenjo-Daro period.

We can relate the decay constant, $λ$ and time t as:

$\frac{N}{N'}$ = $\frac{R'}{R}$ = $e^{- λ t}$

$e^{- λ t} =$ $\frac{R'}{R}$ = $\frac{9}{15}$ = $\frac{3}{5}$

By taking log (ln) on both sides,

$- λ t =$ $\log_{e} ? 3$ - $\log_{e} ? 5$

t = $\frac{0.5108}{λ}$

Since $λ$ = $\frac{0.693}{T_{1 / 2}}$ = $\frac{0.693}{5730}$

t = $\frac{5730 \times 0.5108}{0.693}$ = 4223.5 years

Henc

...more