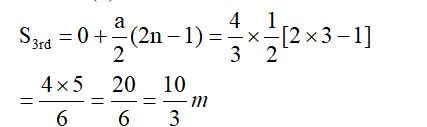3.14 A man walks on a straight road from his home to a market 2.5 km away with a speed of 5 km h–1. Finding the market closed, he instantly turns and walks back home with a speed of 7.5 km h–1.
What is the
(a) Magnitude of average velocity, and
(b) Average speed of the man over the interval of time
(i) 0 to 30 min,
(ii) 0 to 50 min,
(iii) 0 to 40 min?
[Note: You will appreciate from this exercise why it is better to define average speed as total path length divided by time, and not as magnitude of average velocity. You would not like to tell the tired man on his return home that his average speed was zero !]
3.14 A man walks on a straight road from his home to a market 2.5 km away with a speed of 5 km h–1. Finding the market closed, he instantly turns and walks back home with a speed of 7.5 km h–1.
What is the
(a) Magnitude of average velocity, and
(b) Average speed of the man over the interval of time
(i) 0 to 30 min,
(ii) 0 to 50 min,
(iii) 0 to 40 min?
[Note: You will appreciate from this exercise why it is better to define average speed as total path length divided by time, and not as magnitude of average velocity. You would not like to tell the tired man on his return home that his average speed was zero !]
3.14
The distance from home to market = 2.5 km = 2500 m
The speed of the walking while going = 5 kmph = 1.388 m/s
The speed of walking back from market to home = 7.5 kmph = 2.083 m/s
(a) Magnitude of the average velocity = Displacement / time = 0, since the total displacement is zero.
(b)
i. Time taken
Similar Questions for you
Please find the solution below:
[h] = ML2T-1
[E] = ML2T-2
[V] = ML2T-2C-1
[P] = MLT-1
According to question, we can write
10 =
Average speed
(d) Initial velocity
Final velocity
Change in velocity
Momentum gain is along
Force experienced is along
Force experienced is in North-East direction.
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else.
On Shiksha, get access to
Learn more about...

physics ncert solutions class 11th 2023
View Exam DetailsMost viewed information
SummaryDidn't find the answer you were looking for?
Search from Shiksha's 1 lakh+ Topics
Ask Current Students, Alumni & our Experts
Have a question related to your career & education?
See what others like you are asking & answering