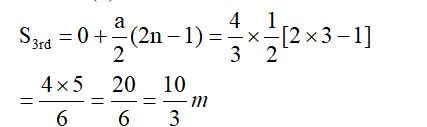3.4 A drunkard walking in a narrow lane takes 5 steps forward and 3 steps backward, followed again by 5 steps forward and 3 steps backward, and so on. Each step is 1m long and requires 1 s. Plot the xt graph of his motion. Determine graphically and otherwise how long the drunkard takes to fall in a pit 13 m away from the start.
3.4 A drunkard walking in a narrow lane takes 5 steps forward and 3 steps backward, followed again by 5 steps forward and 3 steps backward, and so on. Each step is 1m long and requires 1 s. Plot the xt graph of his motion. Determine graphically and otherwise how long the drunkard takes to fall in a pit 13 m away from the start.
3.4
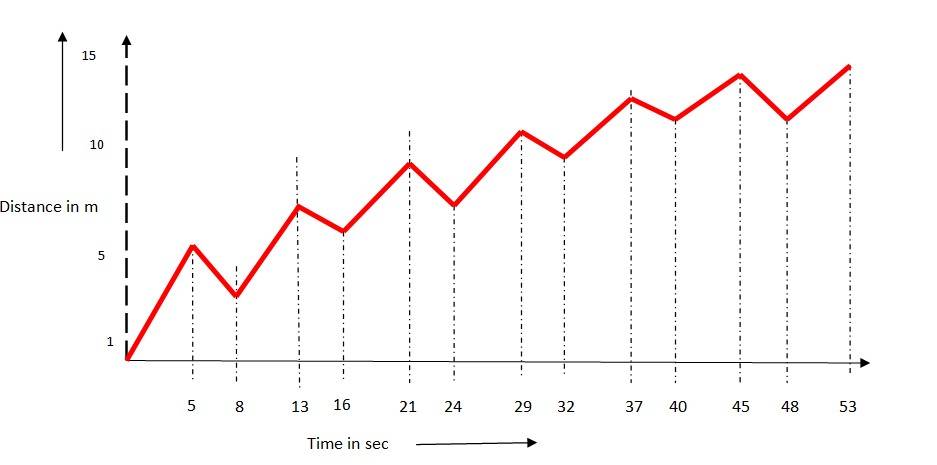
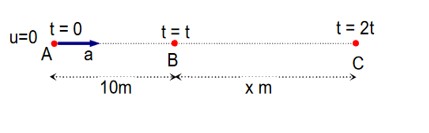
The time taken for each step is 1s, he covers 5 m in 5 secs and goes backward by 3 m in 3 secs.
So in 8 s he covers 2 m. To cover 13m distance he needs to complete 8 m (13-5). To cover 8m, he will require 8 * 4 = 32 s. To fall in a pit, he needs to move another 5m in 5s.
So total time taken = 32 +5
Similar Questions for you
Please find the solution below:
[h] = ML2T-1
[E] = ML2T-2
[V] = ML2T-2C-1
[P] = MLT-1
According to question, we can write
10 =
Average speed
(d) Initial velocity
Final velocity
Change in velocity
Momentum gain is along
Force experienced is along
Force experienced is in North-East direction.
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else.
On Shiksha, get access to
Learn more about...

physics ncert solutions class 11th 2023
View Exam DetailsMost viewed information
SummaryDidn't find the answer you were looking for?
Search from Shiksha's 1 lakh+ Topics
Ask Current Students, Alumni & our Experts
Have a question related to your career & education?
See what others like you are asking & answering