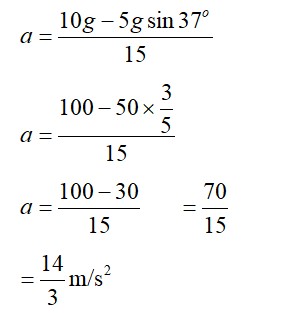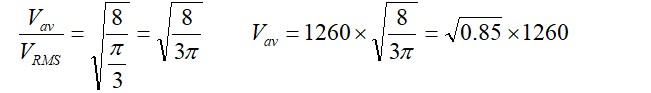5.40 A thin circular loop of radius R rotates about its vertical diameter with an angular frequency . Show that a small bead on the wire loop remains at its lowermost point for . What is the angle made by the radius vector joining the centre to the bead with the vertical downward direction for = ? Neglect friction.
5.40 A thin circular loop of radius R rotates about its vertical diameter with an angular frequency . Show that a small bead on the wire loop remains at its lowermost point for . What is the angle made by the radius vector joining the centre to the bead with the vertical downward direction for = ? Neglect friction.
-
1 Answer
-
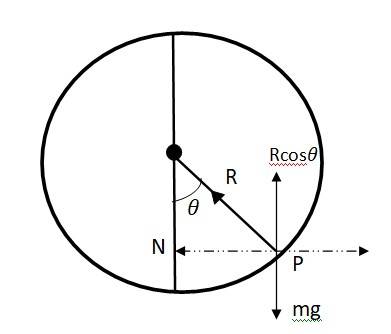
Let be the angle made by the radius vector joining the bead and the centre of the wire with the downward direction. Let, N be the normal reaction.
mg = N …….(1)
mr = N ……(2)
m(R ) = N
Hence N = m(R)
Substituting the value on N in eqn (1)
mg = mR
or = g/ R ………(3)
As 1, the bead will remain at the lowermost point
g/ R
For = becomes
= g/ R
=(g/R)(R/2g) = ½
Similar Questions for you
= 0.92 * 1260 = 1161 m/s
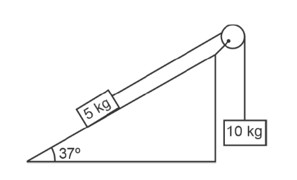
For 2 kg block
T – 2g sin37 = 2a . (i)
For 4 kg block
4g – 2T =
2g – T = a . (ii)
T = (2g – a)
2g – a – 2g * = 2a
3a = 2g *
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers