7.10 (a) Find the moment of inertia of a sphere about a tangent to the sphere, given the moment of inertia of the sphere about any of its diameters to be 2MR ²/5, where M is the mass of the sphere and R is the radius of the sphere.

(b) Given the moment of inertia of a disc of mass M and radius R about any of its diameters to be MR ²/4, find its moment of inertia about an axis normal to the disc and passing through a point on its edge.

25 Views | Posted 4 months ago

Asked by Shiksha User

1 Answer

Answered by

Vishal Baghel | Contributor-Level 10

4 months ago

(a)

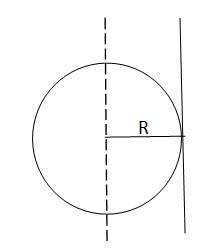
The moment of Inertia of a sphere about its diameter = 2MR ²/5

According to the theorem of parallel axis, the moment of inertia of a body about any axis is equal to the sum of the moment of inertia of the body about a parallel axis passing through its centre of mass and the product of its mass and square of the distance between two parallel axes

Hence the moment of inertia about a tangent of the sphere = 2MR ²/5 + MR² = 7MR ²/5

(b)

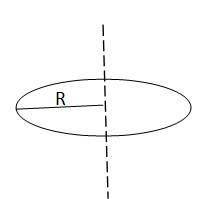
The moment of inertia of a disc about its diameter = MR ²/4

According to the theorem of perpendicular axis, the moment of inertia of a planar body about an axis perpendicular to its plane is equal to t

...more

0 Upvotes 0 Downvotes

Similar Questions for you

The position vector of 1kg object is $\vec{r} = (3 \hat{i} - \hat{j}) m$ and its velocity $\vec{v} = (3 \hat{j} + \hat{k}) m s^{- 1} .$ The magnitude of is angular momentum is $\sqrt[]{x} N m$ where x is________.

Raj Pandey

$\overset{?}{L} = \overset{?}{r} * m \overset{?}{v}$

= $(3 \hat{i} ? \hat{j}) * (3 \hat{j} + \hat{k})$

$= 9 \hat{k} + 3 (? \hat{j}) ? \hat{i}$

$= ? \hat{i} ? 3 \hat{j} + 9 \hat{k}$

$| \overset{?}{L} | = \sqrt[]{1 + 9 + 81} = \sqrt[]{91}$

Match List – I with List – II

Choose the correct answer from the options given below:

Raj Pandey

Use formula for M.I.

A shell of mass $m$ is at rest initially. It explodes into three fragments having mass in the ratio $2 : 2 : 1$ . If the fragments having equal mass fly off along mutually perpendicular directions with speed $v$ , the speed of the third (lighter) fragment is :

Raj Pandey

The angular speed of a fly wheel moving with uniform angular acceleration changes from 1200rpm to 3120 in 16 seconds. The angular acceleration in $r a d / s^{2}$ is:

Raj Pandey

$\begin{array}{r} ω = ω_{0} + α t \\ α = \frac{ω - ω_{0}}{t} \\ = \frac{(3120 - 1200)}{16 s} r p m \\ = \frac{1920}{16} \times \frac{2 π}{60} r a d / s^{2} \\ = 4 π r a d / s^{2} \end{array}$

The ratio of the radius of gyration of a thin uniform disc about an axis passing through its centre and normal to its plane to the radius of gyration of the disc about its diameter is :

Raj Pandey