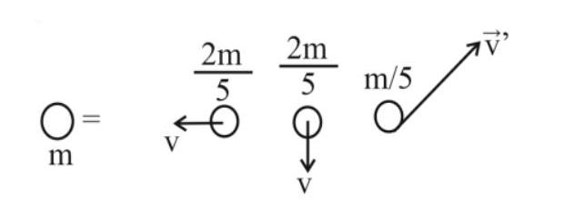
7.13 (a) A child stands at the centre of a turntable with his two arms outstretched. The turntable is set rotating with an angular speed of 40 rev/min. How much is the angular speed of the child if he folds his hands back and thereby reduces his moment of inertia to 2/5 times the initial value ? Assume that the turntable rotates without friction.

(b) Show that the child’s new kinetic energy of rotation is more than the initial kinetic energy of rotation. How do you account for this increase in kinetic energy?

4 Views | Posted 4 months ago

Asked by Shiksha User

1 Answer

Answered by

Vishal Baghel | Contributor-Level 10

4 months ago

(a) Initial angular velocity, $ω$ = 40 rev/min, let the final angular velocity be $ω$

Let the moment of inertia of the boy with hands stretched be I1 and

M.I. with folded hands be I2

Given I2 = (2/5) I1

Since no external force acts on the boy, the angular momentum will remain constant.

Hence I1 $ω$ = I2 $ω_{1}$ , $ω_{2}$ I1/I2) x $ω_{1}$ = (5/2) x 40 = 100 rev/min

(b) Kinetic energy Ev = (1/2)I $ω_{2}$

Hence ( Final KE / Initial KE ) = (I2 $ω_{2} = ($ )/ (I1 $ω_{1}$ ) = { (2/5) I1 x 100 x 100 } / { I1 x 40 x 40 }

= 2.5

0 Upvotes 0 Downvotes

Similar Questions for you

The position vector of 1kg object is $\vec{r} = (3 \hat{i} - \hat{j}) m$ and its velocity $\vec{v} = (3 \hat{j} + \hat{k}) m s^{- 1} .$ The magnitude of is angular momentum is $\sqrt[]{x} N m$ where x is________.

Raj Pandey

$\overset{?}{L} = \overset{?}{r} * m \overset{?}{v}$

= $(3 \hat{i} ? \hat{j}) * (3 \hat{j} + \hat{k})$

$= 9 \hat{k} + 3 (? \hat{j}) ? \hat{i}$

$= ? \hat{i} ? 3 \hat{j} + 9 \hat{k}$

$| \overset{?}{L} | = \sqrt[]{1 + 9 + 81} = \sqrt[]{91}$

Match List – I with List – II

Choose the correct answer from the options given below:

Raj Pandey

Use formula for M.I.

A shell of mass $m$ is at rest initially. It explodes into three fragments having mass in the ratio $2 : 2 : 1$ . If the fragments having equal mass fly off along mutually perpendicular directions with speed $v$ , the speed of the third (lighter) fragment is :

Raj Pandey

The angular speed of a fly wheel moving with uniform angular acceleration changes from 1200rpm to 3120 in 16 seconds. The angular acceleration in $r a d / s^{2}$ is:

Raj Pandey

$\begin{array}{r} ω = ω_{0} + α t \\ α = \frac{ω - ω_{0}}{t} \\ = \frac{(3120 - 1200)}{16 s} r p m \\ = \frac{1920}{16} \times \frac{2 π}{60} r a d / s^{2} \\ = 4 π r a d / s^{2} \end{array}$

The ratio of the radius of gyration of a thin uniform disc about an axis passing through its centre and normal to its plane to the radius of gyration of the disc about its diameter is :

Raj Pandey