7.8 A non-uniform bar of weight W is suspended at rest by two strings of negligible weight as shown in Fig.7.39. The angles made by the strings with the vertical are 36.9° and 53.1° respectively. The bar is 2 m long. Calculate the distance d of the centre of gravity of the bar from its left end.
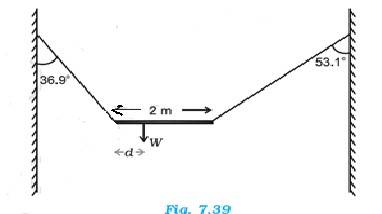
7.8 A non-uniform bar of weight W is suspended at rest by two strings of negligible weight as shown in Fig.7.39. The angles made by the strings with the vertical are 36.9° and 53.1° respectively. The bar is 2 m long. Calculate the distance d of the centre of gravity of the bar from its left end.

A free body diagram needs to be drawn.
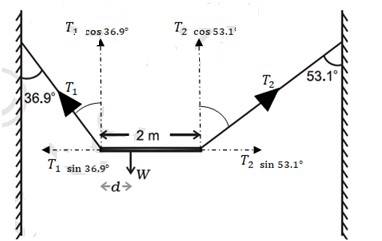
The length of the bar, l = 2 m
T1 and T2
At translational equilibrium, we have =
(T1 / T2) = ( / = 4/3
T1 = (4/3)T2
For rotational equilibrium, on taking the torque about the centre of gravity, we have
T1 x d = T2 (2-d)
T1 x 0.8d = T2 x 0.6 (2-d)
(4/3)T2 x 0.8
Similar Questions for you
Use formula for M.I.
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else.
On Shiksha, get access to
Learn more about...

physics ncert solutions class 11th 2023
View Exam DetailsMost viewed information
SummaryDidn't find the answer you were looking for?
Search from Shiksha's 1 lakh+ Topics
Ask Current Students, Alumni & our Experts
Have a question related to your career & education?
See what others like you are asking & answering