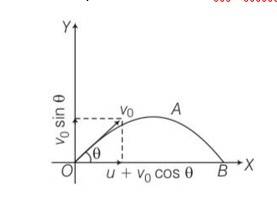
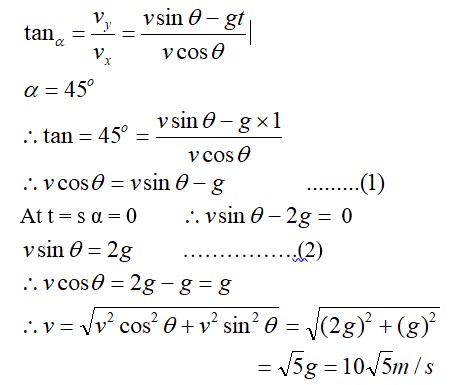A cricket fielder can throw the cricket ball with a speed v_o . If he throws the ball while running with speed u at an angle θ to the horizontal, find

(a) The effective angle to the horizontal at which the ball is projected in air as seen by a spectator.

(b) What will be time of flight?

(c) What is the distance (horizontal range) from the point of projection at which the ball will land ?

(d) Find q at which he should throw the ball that would maximise the horizontal range as found in (iii).

(e) How does q for maximum range change if u >v_o , u = v_o , u < v_o?

(f) How does q in (v) compare with that for u = 0 (i.e.45⁰) ?

3 Views|Posted 7 months ago

Asked by Shiksha User

1 Answer

Sort by:

Answered by

Vishal Baghel | Contributor-Level 10

7 months ago

This is a Long Answer Type Question as classified in NCERT Exemplar

Explanation- a) for x direction u_x= u+v_ocos $θ$

u_y=velocity in y direction= v₀sin $θ$

now tan $θ = \frac{u_{y}}{u_{x}} = \frac{u_{o} s i n θ}{u + u_{o} c o s θ}$

$θ = {t a n}^{- 1} \frac{u_{o} s i n θ}{u + u_{o} c o s θ}$

b) let t be the time flight y =0 u_y=v_osin $θ, a_{y} = - g, t = T$

y= u_yt+1/2 a_yt²

0= v_osin $θ T$ + $\frac{1}{2} (- g T^{2})$

So T = $\frac{2 u_{o} s i n θ}{g}$

c) horizontal range R, = (u+v_ocos $θ$ T= (u+v_ocos $θ$ ) $\frac{2 u_{o} s i n θ}{g}$

d) for range

Upvote

Similar Questions for you

A ball is projected from ground at angle q with the horizontal. After t = 1 s, it is moving at 45° with the horizontal and after t = 2 second, it is moving horizontally. What is speed of projection of ball? [g = 10 m s^–2]

Alok Kumar Singh

Please find the solution below:

An electron in a research apparatus follows a circle path. On the electron’s first circuit of the apparatus, its speed is v₀ and the radius of its circular path is R. Each time it makes on circuit, it passes a short region where it receives a “kick” and gains an additional speed of $\frac{v_{0}}{100} .$ The electron follows a circular path such that the magnitude of its acceleration is always the same. What is the radius of the circular path after the electron has received 10 kicks?

Vishal Baghel

$a = \frac{v_{0}^{2}}{R}$ $\frac{_{}^{}}{}$

after 10 kicks, $v = v_{0} + \frac{10 v_{0}}{100} = 1.1 v_{0}$ $_{} \frac{_{}}{}_{}$

$\Rightarrow R_{1} = 1.21 R$

Two particles start moving from the same point in two different directions. The first particle moves along the positive x-axis with a constant acceleration of 3 m/s². The second particle moves in a straight line making an angle of 60° with the positive x-axis with a constant speed of 24 m/s. Find the time after which the relative velocity of the particles is minimum.

Vishal Baghel

v? = 3tî v? = 24cos 60°î + 24sin 60°? = 12î + 12√3?
v? = v? – v? = (12 – 3t)î + 12√3?
It is minimum when 12 - 3t = 0 ⇒ t = 4sec

A particle is moving in a circle of radius 1m with angular velocity (ω) given as a function of angular displacement ( θ ) by the relation ω = θ² + 2θ. The total acceleration of the particle when θ = 1rad is:


Vishal Baghel

ω = θ² + 2θ
α = (ωdω)/dθ = (θ² + 2θ) (2θ + 2)
At θ = 1rad.
ω = 3rad/s and α = 12rad/s²
a? = αR = 12 m/s² a? = ω²R = 9 m/s² A? = √ (a? ² + a? ²) = 15 m/s²

A flying disc of radius r is moving with constant speed v? while rotating anticlockwise with angular speed v?/r along a curve PQ as shown below. Radius of curvature of curve at the instant is 4r. The magnitude of acceleration of point A at the instant is (3v₀²)/(nr). Find n.

Vishal Baghel

a? = v? ²/4r
a_A? = (v? ²/r²) × r = v? ²/r
a_A = 3v? ²/4r

Taking an Exam? Selecting a College?

Get authentic answers from experts, students and alumni that you won't find anywhere else.

On Shiksha, get access to

66K

Colleges

1.2K

Exams

6.9L

Reviews

1.8M

Answers

Learn more about...

Physics NCERT Exemplar Solutions Class 11th Chapter Four 2025

View Exam Details

Share Your College Life Experience

Didn't find the answer you were looking for?

Search from Shiksha's 1 lakh+ Topics

Ask Current Students, Alumni & our Experts

Quick Actions

Community GuidelinesUser Points System

QuestionsDiscussionsTags

Have a question related to your career & education?

See what others like you are asking & answering