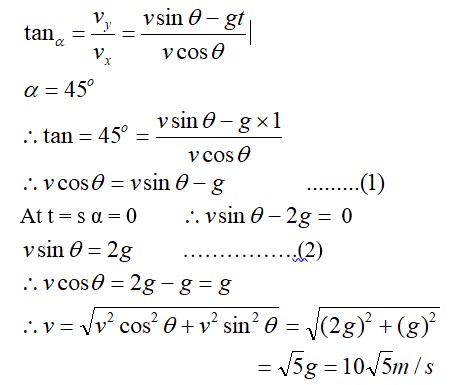A particle is projected in air at an angle β to a surface which itself is inclined at an angle α to the horizontal (Fig).
(a) Find an expression of range on the plane surface (distance on the plane from the point of projection at which particle will hit the surface).
(b) Time of flight.
(c) β at which range will be maximum.
A particle is projected in air at an angle β to a surface which itself is inclined at an angle α to the horizontal (Fig).
(a) Find an expression of range on the plane surface (distance on the plane from the point of projection at which particle will hit the surface).
(b) Time of flight.
(c) β at which range will be maximum.
Similar Questions for you
Please find the solution below:
after 10 kicks,
v? = 3tî v? = 24cos 60°î + 24sin 60°? = 12î + 12√3?
v? = v? – v? = (12 – 3t)î + 12√3?
It is minimum when 12 - 3t = 0 ⇒ t = 4sec
ω = θ² + 2θ
α = (ωdω)/dθ = (θ² + 2θ) (2θ + 2)
At θ = 1rad.
ω = 3rad/s and α = 12rad/s²
a? = αR = 12 m/s² a? = ω²R = 9 m/s² A? = √ (a? ² + a? ²) = 15 m/s²
a? = v? ²/4r
a_A? = (v? ²/r²) * r = v? ²/r
a_A = 3v? ²/4r
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers