A particle moves in a closed orbit around the origin, due to a force which is directed towards the origin. The de-BrOglie wavelength of the particle varies cyclically between two values λ₁, λ₂with λ₁> λ₂ Which of the following statements are true?
(a) The particle could be moving in a circular orbit with origin as centre
(b) The particle could be moving in an elliptic orbit with origin as its focus

(c) When the de-Broglie wavetength is λ₁the particle is nearer the origin than when its value is λ₂
(d) When the de-Broglie wavelength is λ₂ the particle is nearer the origin than when its value is λ₁

Answer-(b,d)

7 Views|Posted 7 months ago

Asked by Shiksha User

1 Answer

Sort by:

Answered by

Alok Kumar Singh | Contributor-Level 10

7 months ago

This is a Multiple Choice Questions as classified in NCERT Exemplar

Explanation- the debroglie wavelength of the particle can be varying cyclically between two values $λ_{1}$ and $λ_{2}$ , if particle is moving in an elliptical orbit with origin as its focus.

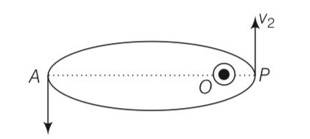
Let v₁, v₂, be the speed of particle at A and B respec

Upvote

Similar Questions for you

Given below are two statements:

Statement I : Davission-Germer experiment establishes, the wave nature of electrons.

Statement II : If electrons have wave nature, they can interfere and show diffraction.

In the light of the above statements choose the correct answer from the option given below:

Raj Pandey

Based on theory

Radiation from hydrogen gas excited to first excited state is used for illuminating certain metallic plate. When the same plate is exposed to the radiation from some unknown hydrogen like gas excited to the same level it is found that de-Broglie wavelength of fastest photoelectron has decreased by 2.3 times. It is given that energy corresponding to longest wavelength of Lyman series of the unknown gas is 3 times the ionization energy of hydrogen gas (13.6eV). The work function (in eV) of the metallic plate is ______. [Take (2.3)² = 5.25]

Vishal Baghel

z² × (13.6) (1 - ¼) = 3 × (13.6)
z = 2 . (i)
h/√2mk? = (1/2.3) × h/√2mk?
=> k? = (2.3)²k? = 5.25k? (ii)
Now, k? = E? - Φ
k? = E? - Φ = z²E? - Φ
∴ k? /k? = (10.2 - Φ)/ (4 × 10.2 - Φ) = 1/5.25
=> Φ = 3eV

Vishal Baghel

$_{} \frac{}{}$ $K . E_{1} = \frac{1230}{800} - ?$ - (i)

$_{}_{} \frac{}{}$ $K . E_{2} = 2 K . E_{1} = \frac{1230}{500} - ?$ - (ii)

from (i) & (ii)

$? = 0.615$ ev

Vishal Baghel

hu = hu₀ + K.E

Cases u = 2u₀

h2u₀ = hu₀ + K.E₁

K.E₁ = hu₀

$\frac{1}{2} m v_{1}^{2} = h υ_{0}$

$v_{1}^{2} = \frac{2 h υ_{0}}{m}$

$v_{1} = \sqrt[]{\frac{2 h υ_{0}}{m}}$ - (1)

Now, cases 2

h 5u₀ = hu₀ + k.E₂

k.E₂ = 4hu₀

$\frac{1}{2} m v_{2}^{2} = 4 h υ_{0}$

v₂ = $\sqrt[]{\frac{8 h υ_{0}}{m}}$ - (2)

$\frac{v_{2}}{v_{1}} = \sqrt[]{\frac{8}{2} = 2}$

v₂ = 2v₁

Kindly consider the following

$f (x) = {\begin{matrix} \frac{2 x^{2} - 3 x + 2}{x - 2}, & x \neq 2 \\ 5, & x = 2 \end{matrix}$

Alok Kumar Singh

This is a Short Answer Type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} f (x) = \frac{2 x^{2} - 3 x - 2}{x - 2} \\ = \frac{2 x^{2} - 4 x + x - 2}{x - 2} = \frac{2 x (x - 2) + 1 (x - 2)}{x - 2} \\ = \frac{(2 x + 1) (x - 2)}{x - 2} = 2 x + 1 \\ \underset{x \to 2^{-}}{l i m} f (x) = 2 x + 1 = \underset{h \to 0}{l i m} 2 (2 - h) + 1 = 4 + 1 = 5 \\ \underset{x \to 2^{+}}{l i m} f (x) = 2 x + 1 = \underset{h \to 0}{l i m} 2 (2 + h) + 1 = 4 + 1 = 5 \\ \underset{x \to 2}{l i m} f (x) = 5 \\ A s \underset{x \to 2^{-}}{l i m} f (x) = \underset{x \to 2^{+}}{l i m} f (x) = \underset{x \to 2}{l i m} f (x) = 5 \\ H e n c e, f (x) i s c o n t i n u o u s a t x = 2 . \end{array}$

Taking an Exam? Selecting a College?

Get authentic answers from experts, students and alumni that you won't find anywhere else.

On Shiksha, get access to

66K

Colleges

1.2K

Exams

6.8L

Reviews

1.8M

Answers

Learn more about...

Physics Ncert Solutions Class 12th 2023

View Exam Details

Share Your College Life Experience

Didn't find the answer you were looking for?

Search from Shiksha's 1 lakh+ Topics

Ask Current Students, Alumni & our Experts

Quick Actions

Community GuidelinesUser Points System

QuestionsDiscussionsTags

Have a question related to your career & education?

See what others like you are asking & answering