Ask & Answer Question

Torque and Angular Momentum Physics System of Particles and Rotational Motion Physics Class 11th

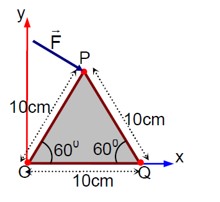
A triangular plate is shown. A force F = 4i - 3j is applied at point P. The torque at point P with respect to point 'O' and 'Q' are :

Option 1 -

15 + 20√3, 15 – 20√3

Option 2 -

-15 - 20√3, 15 – 20√3

Option 3 -

-15 + 20√3, 15 + 20√3

Option 4 -

15 – 20√3, 15 + 20√3

6 Views | Posted a month ago

Asked by Shiksha User

1 Answer

Answered by

Vishal Baghel | Contributor-Level 10

a month ago

Correct Option - 2

Detailed Solution:

Position vector about O (r_o) = 5i + 5√3j

Force vector (F) = 4i - 3j

Torque about O (τ_o) = r_o × F
τ_o = (5i + 5√3j) × (4i - 3j)
τ_o = -15k - 20√3k = (-15 - 20√3)k

Position vector about Q (r_q) = -5i + 5√3j

Torque about Q (τ_q) = r_q × F
τ_q = (-5i + 5√3j) × (4i - 3j)
τ_q = 15k - 20√3k = (15 - 20√3)k

0 Upvotes 0 Downvotes

Similar Questions for you

The dimensions of angular impulse is equal to

alok kumar singh

Angular impulse = Change in angular momentum

[J] = [mvr]

[J] = [M¹L²T^–1]

A thin circular ring of mass M and radius R is rotating with a constant angular velocity 2 rads^-1 in a horizontal plane about an axis vertical to its plane and passing through the centre of the ring. If two objects each of mass m be attached gently to the opposite ends of a diameter of ring, the will then rotate with an angular velocity (in rads^-¹).

Raj Pandey

By conservation of Angular momentum

Li = Lf

$M R^{2} ω = (m R^{2} + 2 m R^{2}) ω'$

$\frac{2 M}{M + 2 m} = ω'$

$\Rightarrow$ $ω' = \frac{2 M}{M + 2 m}$

Consider a 20 kg uniform circular disk of radius 0.2 m. It is pin supported at its centre and is at rest initially. The disk is acted upon by a constant force F = 20 N through a massless string wrapped around its periphery as shown in the figure. Suppose the disk makes n number of revolutions to attain an angular speed of 50 rad s-1. The value of n, to the nearest integer, is ---------.

[Given : In one complete revolution, the disk rotates by 6.28 rad ]

Raj Pandey

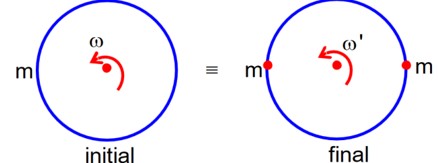
Kindly consider the following Image

A particle of mass 'm' is moving in time 't' on a trajectory given by r? = 10αt² i? + 5β(t-5) j?. Where α and β are dimensional constants. The angular momentum of the particle become the same as it was for t = 0 at time t = ______ seconds.

Raj Pandey

r? = 10αt²î + 5β (t-5)?
v? = dr? /dt = 20αtî + 5β?
As L? = m (r? × v? )
So, at t=0, L=0
given L is same at t=t as at t=0
⇒ r? × v? = 0
⇒ (10αt²î + 5β (t-5)? ) × (20αtî + 5β? ) = 0
⇒ 50αβt² (î×? ) + 100αβt (t-5) (? ×î) = 0
⇒ 50αβt² k? - 100αβt (t-5) k? = 0
⇒ 50t² - 100t (t-5) = 0
⇒ 50t² - 100t² + 500t = 0
⇒ -50t² + 500t = 0
⇒ 50t (10 - t) = 0
⇒ t = 10 second

What is the significance of the direction in torque and angular momentum?

Syed Aquib Ur Rahman

The direction of torque and angular momentum defines how and in which orientation an object will rotate or sustain its spin. This is important to understand in machines, athletic movements, and even natural phenomena, such as planetary motion.

Get authentic answers from experts, students and alumni that you won't find anywhere else

On Shiksha, get access to

65k Colleges
1.2k Exams
688k Reviews
1800k Answers

Community GuidelinesUser Points System

QuestionsDiscussionsTags

A triangular plate is shown. A force F = 4i - 3j is applied at point P. The torque at point P with respect to point 'O' and 'Q' are :

1 Answer

Similar Questions for you

Learn more about...

Most viewed information

Share Your College Life Experience

Didn't find the answer you were looking for?

Need guidance on career and education? Ask our experts

Your Question