A uniform disc of radius R, is resting on a table on its rim. The coefficient of friction between disc and table is µ (Fig). Now the disc is pulled with a force F as shown in the figure. What is the maximum value of F for which the disc rolls without slipping ?
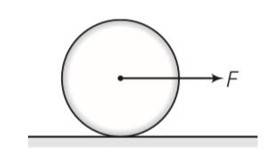
A uniform disc of radius R, is resting on a table on its rim. The coefficient of friction between disc and table is µ (Fig). Now the disc is pulled with a force F as shown in the figure. What is the maximum value of F for which the disc rolls without slipping ?

This is a long answer type question as classified in NCERT Exemplar
Frictional force f is acting in the opposite direction of F . let the acceleration of centre of mass of disc be a then
F-f=Ma where M is the mass of the disc
fR= (1/2 MR2)
so fR= (1/2MR2) (a/R)
Ma=2f
From the above equation
F = F/3
F<
Similar Questions for you
Use formula for M.I.
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else.
On Shiksha, get access to
Learn more about...

Physics NCERT Exemplar Solutions Class 11th Chapter Seven 2025
View Exam DetailsMost viewed information
SummaryDidn't find the answer you were looking for?
Search from Shiksha's 1 lakh+ Topics
Ask Current Students, Alumni & our Experts
Have a question related to your career & education?
See what others like you are asking & answering