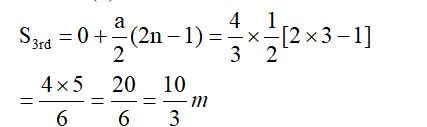For the one-dimensional motion, described by x = t–sint
(a) x (t) > 0 for all t > 0.
(b) v (t) > 0 for all t > 0.
(c) a (t) > 0 for all t > 0.
(d) v (t) lies between 0 and 2.
For the one-dimensional motion, described by x = t–sint
(a) x (t) > 0 for all t > 0.
(b) v (t) > 0 for all t > 0.
(c) a (t) > 0 for all t > 0.
(d) v (t) lies between 0 and 2.
-
1 Answer
-
This is a multiple choice answer as classified in NCERT Exemplar
(a, d) x= t-sint
Velocity v = dx/dt=
d/dt (t-sint)=
=1-cost
When cost =1, velocity v=0
Vmax=1-costmin = 1- (-1)=2
Vmin =1- (cost)max= 1-1=0
Hence v lies between 0 and 2
Acceleration a=dv/dt=-sint
When v=0 then cost =1
Vmax= 1- (-1)=2, Vmin=1-1=0
Similar Questions for you
Please find the solution below:
[h] = ML2T-1
[E] = ML2T-2
[V] = ML2T-2C-1
[P] = MLT-1
According to question, we can write
10 =
Average speed
(d) Initial velocity
Final velocity
Change in velocity
Momentum gain is along
Force experienced is along
Force experienced is in North-East direction.
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers