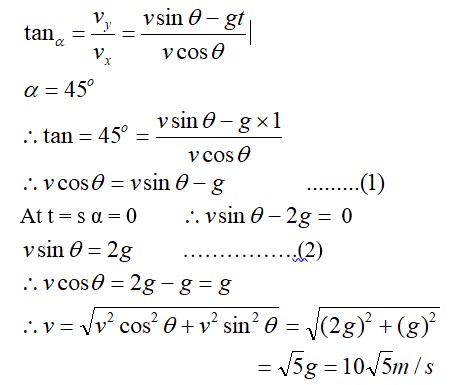Q.4.21 A particle starts from the origin at t = 0 s with a velocity of 10.0 ? m/s and moves in the x-y plane with a constant acceleration of (8.0 ? + 2.0 ?) m s-2.
(a) At what time is the x- coordinates of the particle 16 m? What is the y-coordinate of the particle at that time?
(b) What is the speed of the particle at the time?
Q.4.21 A particle starts from the origin at t = 0 s with a velocity of 10.0 ? m/s and moves in the x-y plane with a constant acceleration of (8.0 ? + 2.0 ?) m s-2.
(a) At what time is the x- coordinates of the particle 16 m? What is the y-coordinate of the particle at that time?
(b) What is the speed of the particle at the time?
-
1 Answer
-
Ans.4.21:
(a) Velocity , = 10.0 ? m/s
Acceleration, = (8.0 ? + 2.0 ?) m s-2
We know = = 8.0 ? + 2.0 ?
= (8.0 ? + 2.0 ?)dt
Integrating both sides we get (t) = 8.0t ? + 2.0t ? + ,
Where, velocity vector of the particle at t =0
velocity vector of the particle at time t
But =
= dt
= (8.0t ? + 2.0t ? + )dt
Integrating both sides with the condition at t = 0, r =0 and at t =t, r = r
t + ½ 8.0 t2 ? + ½ 2.0 t2 ? = t + 4.0 t2 ? + t2 ?
Substituting the value of , we get
( 10.0 ?)t + 4.0 t2 ? + t2 ? . This equation can be expressed as
x ? + y ? = 4.0 t2 ? + ( 10.0t + t2) ?
Since the motion of the particle is confined to the x-y plane, on equating the coefficients of ? and ?, we get
x = 4.0 t2 and y = 10.0t + t2
t =
(a) When x = 16m, t = 2 s, y = 24m
(b) Velocity of the particle
(t) = 8.0t ? + 2.0t ? +
At t = 2 s,
(t) = 8.0 2 ? + 2.0 ? + 10 ? = 16 ? + 14 ?
The magnitude of (t) is given by
= ( 162 + 142)1/2 = 21.26 m/s
Similar Questions for you
Please find the solution below:
after 10 kicks,
v? = 3tî v? = 24cos 60°î + 24sin 60°? = 12î + 12√3?
v? = v? – v? = (12 – 3t)î + 12√3?
It is minimum when 12 - 3t = 0 ⇒ t = 4sec
ω = θ² + 2θ
α = (ωdω)/dθ = (θ² + 2θ) (2θ + 2)
At θ = 1rad.
ω = 3rad/s and α = 12rad/s²
a? = αR = 12 m/s² a? = ω²R = 9 m/s² A? = √ (a? ² + a? ²) = 15 m/s²
a? = v? ²/4r
a_A? = (v? ²/r²) * r = v? ²/r
a_A = 3v? ²/4r
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers