Ask & Answer Question

Moment of Inertia Physics System of Particles and Rotational Motion Physics Class 11th

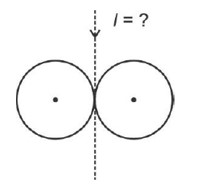
The linear mass density of a thin rod AB of length L varies from A to B as λ(x) = λ₀ (1 + x/L), where x is the distance from A. If M is the mass of the rod then its moment of inertia about an axis passing through A and perpendicular to the rod is:

Option 1 -

(5/12)ML²

Option 2 -

(7/18)ML²

Option 3 -

(2/5)ML²

Option 4 -

(3/5)ML²

4 Views | Posted a month ago

Asked by Shiksha User

1 Answer

Answered by

alok kumar singh | Contributor-Level 10

a month ago

Correct Option - 2

Detailed Solution:

dm = λdx = λ? (1 + x/L)dx
M = ∫? λ? (1 + x/L)dx = λ? [L + L²/2L] = 3λ? L/2
dI = dmx² = λ? (1 + x/L)dx × x²
I = λ? ∫? (x² + x³/L)dx = λ? [L³/3 + L? /4L]
I = (7λ? L³)/12 = (7/12) * (2M/3L) * L³ = (7/18)ML²

0 Upvotes 0 Downvotes

Similar Questions for you

Two solid spheres each of mass 2 kg and radius 75 cm are arranged as shown. Find MOI of the system about the given axis.

alok kumar singh

$I = (\frac{2}{5} M R^{2} + M R^{2}) \times 2$

$= \frac{14}{5} \times 2 \times \frac{9}{16}$

$= \frac{63}{20}$

= 3.15 kg m²

Two particles of masses 5 kg and 10 kg are placed along x-axis at positions x = 1 m and x = 3 m. The moment of inertia of the system about an axis respectively passing through centre of mass and parallel to y-axis is

alok kumar singh

Distance of CM from 5 kg = 10*2/15 = 4/3m

Two circular rings (of same material) are of same thickness. The diameter of first ring is twice that of second. The moment of inertia of first ring as compared to that of second is

alok kumar singh

Moment of inertia of a system made from three uniform rods each of mass m and length l joined to each other, as shown in the figure about one end O and perpendicular to its plane will be

Raj Pandey

The momentum of inertia of a uniform thin rod about a perpendicular axis passing through on end is I1. The same rod is into a ring and its moment of inertia about a diameter is I2. If $\frac{I_{1}}{I_{2}} i s \frac{X π^{2}}{3},$ $\frac{_{}}{_{}} \frac{^{}}{}$ then the value of x will be__________.

Vishal Baghel

According to question, we can write

$l = 2 π r \Rightarrow r = \frac{l}{2 π}$

$I_{1} = \frac{m l^{2}}{3}, a n d I_{2} = \frac{m r^{2}}{2} = \frac{m l^{2}}{8 π^{2}}$

$\Rightarrow \frac{I_{1}}{I_{2}} = \frac{m l^{2}}{3} \times \frac{8 π^{2}}{m l^{2}} = \frac{8 π^{2}}{3}$

Get authentic answers from experts, students and alumni that you won't find anywhere else

On Shiksha, get access to

65k Colleges
1.2k Exams
688k Reviews
1800k Answers

Community GuidelinesUser Points System

QuestionsDiscussionsTags

The linear mass density of a thin rod AB of length L varies from A to B as λ(x) = λ₀ (1 + x/L), where x is the distance from A. If M is the mass of the rod then its moment of inertia about an axis passing through A and perpendicular to the rod is:

1 Answer

Similar Questions for you

Learn more about...

Most viewed information

Share Your College Life Experience

Didn't find the answer you were looking for?

Need guidance on career and education? Ask our experts

Your Question