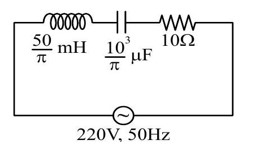
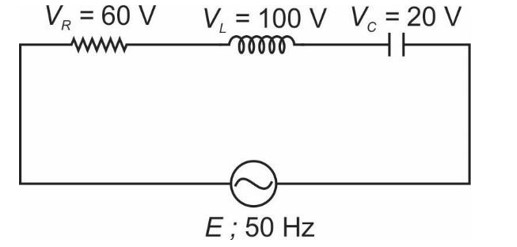
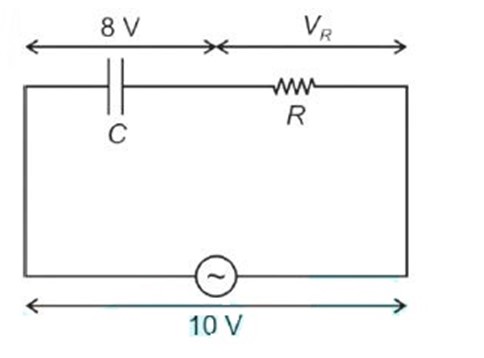
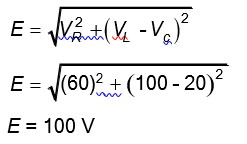Physics Alternating Current Class 12th Physics Power in AC Circuit

The net impedance of circuit (as shown in figure) will be:

Option 1 - <p><span class="mathml" contenteditable="false"> <math> <mn>25</mn> <mtext> </mtext> <mi mathvariant="normal">W</mi> </math> </span></p>

Option 2 - <p><span class="mathml" contenteditable="false"> <math> <mn>10</mn> <mroot> <mrow> <mrow> <mn>2</mn> </mrow> </mrow> <mrow></mrow> </mroot> <mi mathvariant="normal">Ω</mi> </math> </span></p>

Option 3 - <p><span class="mathml" contenteditable="false"> <math> <mn>15</mn> <mtext> </mtext> <mi mathvariant="normal">W</mi> </math> </span></p>

Option 4 - <p><span class="mathml" contenteditable="false"> <math> <mn>5</mn> <mroot> <mrow> <mrow> <mn>5</mn> </mrow> </mrow> <mrow></mrow> </mroot> <mi mathvariant="normal">Ω</mi> </math> </span></p>

7 Views|Posted 5 months ago

Asked by Shiksha User

1 Answer

Sort by:

R

Answered by

Raj Pandey | Contributor-Level 9

5 months ago

Correct Option - 4

Detailed Solution:

$ω = 2 π f \Rightarrow ω = 100 π$

$Z = \sqrt[]{R^{2} + {(X_{L} - X_{C})}^{2}}$

$= \sqrt[]{10^{2} + {(ω L - \frac{1}{ω C})}^{2}}$

$= \sqrt[]{100 + {(100 π * \frac{50}{π} * 10^{- 3} - \frac{1}{100 π * \frac{10^{3}}{π} * 10^{- 6}})}^{2}}$

$= \sqrt[]{100 + (5 - 10)^{2}}$

$= \sqrt[]{100 + 25}$

$Z = 5 \sqrt[]{5} Ω$

Upvote

Thumbs Down Icon

Similar Questions for you

An alternating potential V=V₀sin wt is applied across a circuit. As a result the current I=I₀Sin $I = I_{0} sin (ω t - \frac{π}{2})$ flows in it. The power consumed in the circuit per cycle is

No power consumed without any resistance.

An AC source rated 220 V, 50Hz is connected to a resistor. The time taken by the current to change from its maximum to the rms value is :


T = 2π√ (l/g) ⇒ g = 4π²l/T²
Percentage error: Δg/g = Δl/l + 2 (ΔT/T) = (0.1/10.0) + 2 (0.005/0.5) = 0.03
Percentage error = (Δg/g) × 100 = 3%
ω = 2πf = 100π rad/s
i_rms = i? /√2
While current changes from its maximum to its rms value, its phase changes by π/4 rad.
t = (π/4)/ω = π/ (4 × 100π) = 2.5 × 10? ³

An electric bulb and a capacitor are connected in series with an AC source. On increasing the frequency of the source, the brightness of the bulb:

Alok Kumar Singh

X_C = 1/ ωC

On increasing w; XC decreases so Z decreases, current in circuit increases.

The value of alternating emf (E) in the given circuit will be

Alok Kumar Singh

In a series $C - R$ circuit shown in figure, the applied voltage is $10 V$ and the voltage across $R$ the capacitor is found to be . The voltage across and the phase difference between current and the applied voltage will be respectively.

Alok Kumar Singh

$A s V^{2} = V_{R}^{2} + C_{C}^{2}$

$? V_{R} = \sqrt[]{V^{2} - V_{C}^{2}} = \sqrt[]{10^{2} - 8^{2}} = 6 V$

$\tan ? θ = \frac{X_{C}}{X_{R}} = \frac{V_{C}}{V_{R}} = \frac{8}{6} = \frac{4}{3}$

Now,

Taking an Exam? Selecting a College?

Get authentic answers from experts, students and alumni that you won't find anywhere else.

On Shiksha, get access to

66K

Colleges

|

1.2K

Exams

|

6.9L

Reviews

|

1.8M

Answers

Learn more about...

Physics Alternating Current 2025

Physics Alternating Current 2025

View Exam Details

Most viewed information

Share Your College Life Experience

Didn't find the answer you were looking for?

Search from Shiksha's 1 lakh+ Topics

or

Ask Current Students, Alumni & our Experts

Quick Actions

Community GuidelinesUser Points System

QuestionsDiscussionsTags

Have a question related to your career & education?

or

See what others like you are asking & answering