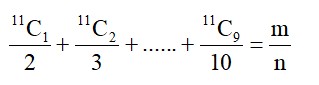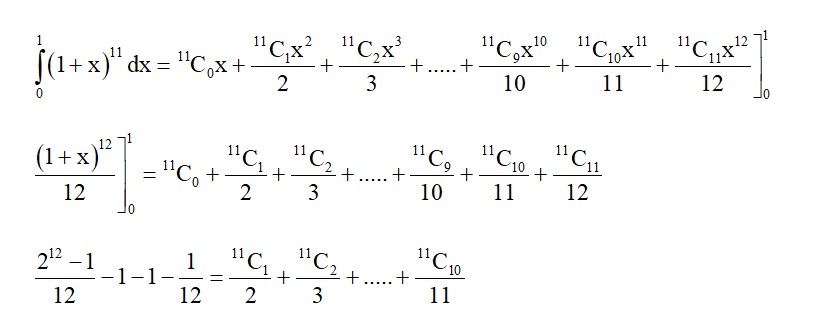Ask & Answer: India's Largest Education Community
All Questions
New Question
a month agoContributor-Level 10
Start with
(1)
(2)
(3) GTE : 4!, GTN: 4!, GTT : 4!
(4) GTWENTY = 1
⇒ 360 + 60 + 60 + 24 + 24 + 24 + 1 = 553
New Question
a month agoNew Question
a month agoContributor-Level 10
->g(x) = |x|, x Î (–3, 1)
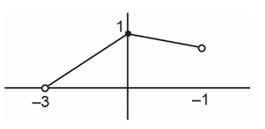
Range of fog(x) is [0, 1]
Range of fog(x) is [0, 1]
New Question
a month agoContributor-Level 10
Reflexive :for (a, b) R (a, b)
-> ab– ab = 0 is divisible by 5.
So (a, b) R (a, b) " a, b Î Z
R is reflexive
Symmetric:
For (a, b) R (c, d)
If ad – bc is divisible by 5.
Then bc – ad is also divisible by 5.
-> (c, d) R (a, b) "a, b, c, dÎZ
R is symmetric
Transitive:
If (a, b) R (c, d) ->ad –bc divisible by 5 and (c, d) R (e, f) Þcf – de divisible by 5
ad – bc = 5k1 k1 and k2 are integers
cf– de = 5k2
afd – bcf = 5k1f
bcf – bde = 5k2b
afd – bde = 5 (k1f + k2b)
d (af– be) = 5 (k1f + k2b)
-> af – be is not divisible by 5 for every a, b,
New Question
a month agoContributor-Level 10
First term = a
Common difference = d
Given: a + 5d = 2 . (1)
Product (P) = (a1a5a4) = a (a + 4d) (a + 3d)
Using (1)
P = (2 – 5d) (2 – d) (2 – 2d)
-> = (2 – 5d) (2 –d) (– 2) + (2 – 5d) (2 – 2d) (– 1) + (– 5) (2 – d) (2 – 2d)
= –2 [ (d – 2) (5d – 2) + (d – 1) (5d – 2) + (d – 1) (5d – 2) + 5 (d – 1) (d – 2)]
= –2 [15d2 – 34d + 16]
at
-> d = 1.6
New Question
a month agoContributor-Level 10
16cos2θ + 25sin2θ + 40sinθ cosθ = 1
16 + 9sin2θ + 20sin 2θ = 1
+ 20sin 2θ = 1
– 9cos 2θ + 40sin 2θ = – 39
48tan2θ + 80tanθ + 30 = 0
24tan2θ + 40tanθ + 15 = 0
-> ,
So will be rejected as
Option (4) is correct.
New Question
a month agoContributor-Level 10
The institute asks for an application fee worth AED 250. This is around INR 5,900. The applicants can apply to this university by following the direct university link. A few of the documents that have to be submitted along with the application are:
- Academic transcripts of the qualifications
- IELTS / TOEFL score
- Copy of the passport
Documents required for Doctoral courses
- Academic transcripts (Master's degree)
Resume / CV - Research proposal
- Work experience letter
- Reference letters from employers and the university
- Passport copy
New Question
a month agoContributor-Level 10
IF =
So, y(1 + cos2 x) =
y(1 + cos2 x) = – cos x + c
y(0) = 0
0 = – 1 + c
-> c = 1
Now,
New Question
a month agoContributor-Level 10
a, ar, ar2, ….ar63
a+ar+ar2 +….+ar63 = 7 [a + ar2 + ar4 +.+ar62]
1 + r = 7
r = 6
New Question
a month agoContributor-Level 10
|2A| = 27
8|A| = 27
Now |A| = α2–β2 = 24
α2 = 16 + β2
α2– β2 = 16
(α–β) (α+β) = 16
->α + β = 8 and
α – β = 2
->α = 5 and β = 3
New Question
a month agoContributor-Level 10
The SLAT exam will comprise a total of 60 questions which will be required to be answered in 60 minutes (1 hour). There will be five sections in SLAT 2026 exam and each section will have 12 questions. Candidates must practice previous year papers and sample papers to understand the structure of exam and level of questions asked in exam.
New Question
a month agoContributor-Level 10
12x =
is the solution of above equation.
Statement 1 is true
f(0) = – 1 < 0
one root lies in , one root is which is positive. As the coefficients are real, therefore all the roots must be real.
Statement 2 is false.
New Question
a month agoContributor-Level 10
Yes, the institute can be considered a good institute for higher studies abroad. The institute offers more than 40 internationally accredited degrees, licensed by the KHDA. The faculty is well-versed, and the institute enrolls more than 3,500 students from 108 countries.
New Question
a month agoBeginner-Level 5
Psychology students at Chandigarh University enjoy an engaging and well-rounded campus life. The university offers academic support through advanced labs, counseling centers, and research facilities while promoting extracurricular involvement through student clubs, events, and national-level competitions. Interaction with peers, participation in seminars, and field visits provide practical exposure, enhancing learning beyond the classroom. Hostel facilities, transport services, dining options, and recreational amenities contribute to convenience and comfort. This combination of academic, social, and professional activities ensures stud
Register to get relevant
Questions & Discussions on your feed
Ask & Answer
Panel of Experts