Ask & Answer: India's Largest Education Community

$h=\frac{2Scos\theta }{\rho gR}$

as T­, S¯

The correct answer is Option (2).

  $\frac{GMm}{{\left(R+x\right)}^2}=\frac{GMm\left(R-x\right)}{R^3}$

->R³ = (R + x)² (R – x)

->R³ = (R²– x²) (R + x)

->x² + Rx – R² = 0

$x=\frac{-R\pm \sqrt[]{R+4R^2}}{2}$

$x=\frac{\left(\sqrt[]{5R}-1\right)}{2}R$

  $\frac{v^2}{2a}=s$ (a = mg)

v² = 2 × mgs

v² = 2 × (0.4) × 10 × 10

v² = 80

W_f = Dk

= $-\frac{1}{2}\times 100\times 80$  

W_f = – 4000

NJIT acceptance rate is around 65%, meaning that out of every 100 students who apply to the university's admission process, around 65 are likely to be offered the opportunity to enroll on the campus grounds. This makes the admission criteria moderately selective.

n P (A) = 2⁷ = 128

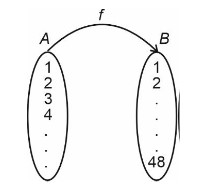
f : A → B

Number of function = 128 × 128….128 = 128⁷

$={\left(2^7\right)}^7=2^{49}$

->mⁿ = 2⁴⁹

m + n = 49 + 2 = 51

$N={\displaystyle \sum _{}^{}f}=27$

$\left(\frac{N}{2}\right)=\frac{27}{2}=13.5$

So, we have median lies in the class 12 – 16

I₁ = 12, f = 8, h = 4, c.f. = 13

So, here we apply formula

$M=I_1+\frac{\frac{N}{2}-c.f.}{f}\times h=12+\frac{13.5-13}{8}\times 4$

$=12+\frac{5}{2}$

$M=\frac{24.5}{2}=12.25$

20 M = 20 × 12.25

= 245

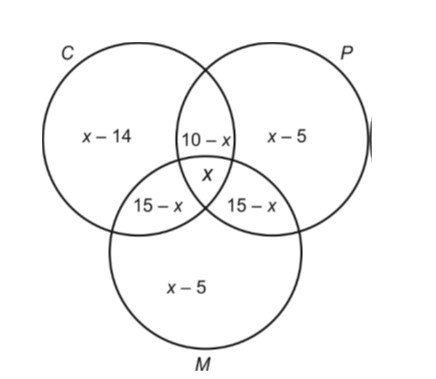
n (C) = 16, n (P) = 20, n (M) = 25

n (MÇP) = n (MÇC) = 15, n (PÇC) = 10,

n (MÇCÇP) = x.

n (CÈPÈM) £ n (U) = 40

n (CÈPÈM) = n (C) + n (P) + n (M) – n (C? M) – n (PÈM) – n (CÇP) + n (CÇPÇM)

40 ³ 16 + 20 + 25 – 15 – 15 – 10 + x

40 ³ 61 – 40 + x

19 ³ x

So maximum number of students that passed all the exams is 19.

$I=9{\displaystyle \underset{0}{\overset{9}{\int }}\left[\sqrt[]{\frac{10x}{x+1}}\right]dx}$

$=9\left[{\displaystyle \underset{0}{\overset{1/9}{\int }}0dx}+{\displaystyle \underset{1/9}{\overset{2/3}{\int }}dx}+{\displaystyle \underset{2/3}{\overset{9}{\int }}2dx}\right]$

$=9\left[\frac{2}{3}-\frac{1}{9}+2\left[9-\frac{2}{3}\right]\right]$

$=9\left[\frac{5}{9}+2\times \frac{25}{3}\right]$

= 5 + 6 × 25

= 5 + 150

= 155

$T_{n+1}={}^n{C}_{r}11^{\frac{1}{6}}\cdot 7^{\frac{824-4}{2}}$

For integral term

6 should divide r

and  $\frac{824-r}{2}$  must be integer

->2 most divide r

->r divisible by 6

->possible values of r Î {0, 1, 2, …824}

->For integer terms

r Î {0, 6, 12, …822} (822 = 0 + (n – 1)6 Þ n = 138)

= 138 terms

If x = 0, y = 6, 7, 8, 9, 10

If x = 1, y = 7, 8, 9, 10

If x = 2, y = 8, 9, 10

If x = 3, y = 9, 10

If x = 4, y = 10

If x = 5, y = no possible value

Total possible ways = (5 + 4 + 3 + 2 + 1) * 2

= 30

Required probability  $=\frac{30}{11*11}=\frac{30}{121}$

Given $\left|\overrightarrow{a}\right|=1$ , $\left|\overrightarrow{b}\right|=4$ , $\overrightarrow{a}\cdot \overrightarrow{b}=2$

$\overrightarrow{c}=2\left(\overrightarrow{a}\times \overrightarrow{b}\right)-3\overrightarrow{b}$  

Dot product with  $\overrightarrow{a}$ on both sides

$\overrightarrow{c}\cdot \overrightarrow{a}=-6$ . (1)

Dot product with  $\overrightarrow{b}$  on both sides

$\overrightarrow{b}\cdot \overrightarrow{c}=-48$ . (2)

$\overrightarrow{c}\cdot \overrightarrow{c}=4{\left|\overrightarrow{a}\times \overrightarrow{b}\right|}^2+9{\left|\overrightarrow{b}\right|}^2$

${\left|\overrightarrow{c}\right|}^2=4\left[{\left|\overrightarrow{a}\right|}^2\cdot {\left|\overrightarrow{b}\right|}^2-{\left(\overrightarrow{a}\cdot \overrightarrow{b}\right)}^2\right]+9{\left|\overrightarrow{b}\right|}^2$

${\left|\overrightarrow{c}\right|}^2=4\left[\left(1\right){\left(4\right)}^2-\left(4\right)\right]+9\left(16\right)$

${\left|\overrightarrow{c}\right|}^2=4\left[12\right]+144$

${\left|\overrightarrow{c}\right|}^2=48+144$

${\left|\overrightarrow{c}\right|}^2=192$

$cos\theta =\frac{\overrightarrow{b}\cdot \overrightarrow{c}}{\left|\overrightarrow{b}\right|\left|\overrightarrow{c}\right|}$

$cos\theta =\frac{-48}{\sqrt[]{192}\cdot 4}$

$cos\theta =\frac{-48}{8\sqrt[]{3}\cdot 4}$

$cos\theta =\frac{-3}{2\sqrt[]{3}}$

$cos\theta =\frac{-\sqrt[]{3}}{2}$ $\theta =co{s}^{-1}\left(\frac{-\sqrt[]{3}}{2}\right)$

$z^2=-\overline{iz}$

$\left|z^2\right|=\left|-\overline{iz}\right|$

$\left|z^2\right|=\left|z\right|$

$\left|z^2\right|-\left|z\right|=0$

$\left|z\right|\left(\left|z\right|-1\right)=0$

|z| = 0 (not acceptable)

|z| = 1

|z|² = 1

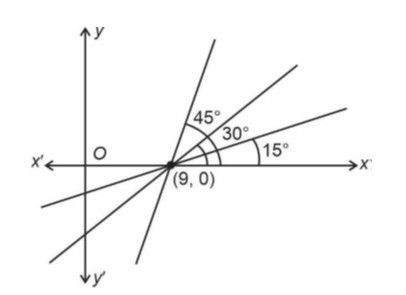
Eqⁿ : y – 0 = tan45° (x – 9) Þ y = (x – 9)

Option (B) is correct

Given : x² – 70x + l = 0

->Let roots be a and b

->b = 70 – a

->= a (70 – a)

l is not divisible by 2 and 3

->a = 5, b = 65

-> $\frac{\sqrt[]{5-1}+\sqrt[]{65-1}}{\left|60\right|}=\left|\frac{4+8}{60}\right|=\frac{1}{5}$

$\frac{dy}{dx}=\frac{\left(x+1\right)\left(x^2-x+1\right)+\sqrt[]{\left(1-x\right)\left(1+x\right)}}{\left(x-1\right)\left(x+1\right)}$

$\frac{dy}{dx}=\frac{x\left(x-1\right)+1}{\left(x-1\right)}+\sqrt[]{\frac{\left(1-x\right)\left(1+x\right)}{{\left(x-1\right)}^2{\left(x+1\right)}^2}}$

$\frac{dy}{dx}=x+\frac{1}{x-1}+\frac{1}{\sqrt[]{\left(1-x\right)\left(1+x\right)}}$

$dy=xd+\frac{1}{\left(x-1\right)}dx+\frac{dx}{\sqrt[]{1-x^2}}$

$y=\frac{x^2}{2}+ln\left|x-1\right|+si{n}^{-1}x+c$

at x = 0, y = 2 2 = c

$y=\frac{x^2}{2}+ln\left|x-1\right|+si{n}^{-1}x+2$

$y\left(\frac{1}{2}\right)=\frac{17}{8}+\frac{\pi }{6}-ln2$

-> $-1\le \left|\begin{array}{cc}\hfill \overline{2-\left|x\right|}\hfill & \hfill 4\hfill \end{array}\right|\le 1$

-> $\left|\frac{2-\left|x\right|}{4}\right|\le 1$

$-1\le \frac{2-\left|x\right|}{4}\le 1$

–4 £ 2 – |x| £ 4

–6 £ – |x| £ 2

–2 £ |x| £ 6

|x| £ 6

->x Î [–6, 6]              …(1)

Now, 3 – x ¹ 1

And x ¹ 2                    …(2)

and 3 – x > 0

x < 3                            …(3)

From (1), (2) and (3)

->x Î [–6, 3] – {2}

a = 6

b = 3

g = 2

a + b + g = 11

$f\text{'}\left(x\right)=\frac{g\text{'}\left(x\right)-g\text{'}\left(2-x\right)}{2},f\text{'}\left(\frac{3}{2}\right)=\frac{g\text{'}\left(\frac{3}{2}\right)-g\text{'}\left(\frac{1}{2}\right)}{2}=0$  

Also  $f\text{'}\left(\frac{1}{2}\right)=\frac{g\text{'}\left(\frac{1}{2}\right)-g\text{'}\left(\frac{3}{2}\right)}{2}=0$ , f' (1) = 0

-> $f\text{'}\left(\frac{3}{2}\right)=f\text{'}\left(\frac{1}{2}\right)=0$  

->roots in $\left(\frac{1}{2},1\right)$ and $\left(1,\frac{3}{2}\right)$  

->f" (x) is zero at least twice in $\left(\frac{1}{2},\frac{3}{2}\right)$

$?$ ae = 2b

$\frac{4b^2}{a^2}=e^2$  

Or 4 (1 – e²) = e²

4 = 5e² -> $e=\frac{2}{\sqrt[]{5}}$