What are the key formulas in Conic Sections?
-
1 Answer
-
Those who are preparing for any competive exam such as JEE Main, NDA and others really need to memorise formulas. Check the important formulas below;
Circle
Standard equation (center at origin):
General form:
Center = (–g, –f), Radius = ?(g² + f² – c)
Parabola:
Standard form (horizontal axis):
Standard form (vertical axis):
Vertex: (0, 0)
Focus: (a, 0) or (0, a)
Directrix: x = –a or y = –a
Latus rectum = 4a
Ellipse: Check all the important topics related to this topic below;
- Standard form (major axis along x-axis):
where a > b
Eccentricity:
Foci: (±ae, 0)
Latus rectum:
Hyperbola: Students can check impor
...more
Similar Questions for you
Given 2a + 2b =
4b2 = 7a2
b =
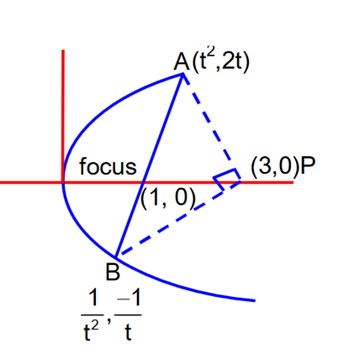
Tangent to C1 at (-1, 1) is T = 0
x(-1) + 4(1) = 2
-x + y = 2
find OP by dropping from (3, 2) to centre
OP =
AP =
area of
AN =
sin =
M1 M2 = 1
t = 1
So, A (1, 2) and B (1, 2) they must be end pts of focal chord.
Length of latus rectum
b2 = 2a and ae = 1
Eccentricity of ellipse (Horizontal)
b2 = a2 (1 – e2)
2a = a2 (1 – e2)
2 =
e2 + 2e – 1 = 0
now
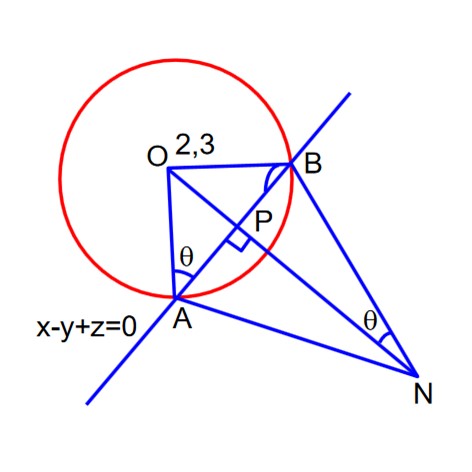
Given hyperbola : so eccentricity e = and directrices
k = 2 therefore equation of hyperbola is
hence it passes through the point
Abscissae of PQ are roots of x2 – 4x – 6 = 0
Ordinates of PQ are roots of y2 + 2y – 7 = 0 and PQ is diameter
Equation of circle is
But, given
By comparison a = -2, b = 1, c = -13 Þ a + b – c = -2 + 1 + 13 = 12
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers