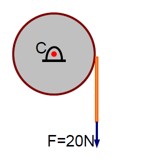
A pulley of radius 1.5m is rotated about its axis by a force F = (12t – 3t²)N applied tangentially (while t is measured in seconds). If moment of inertia of the pulley about its axis of rotation is 4.5 kg m², the number of rotation made by the pulley before its direction of motion is reversed, will be $\frac{K}{π} .$ The value of K is ________.

14 Views|Posted 6 months ago

Asked by Shiksha User

1 Answer

Sort by:

Answered by

Payal Gupta | Contributor-Level 10

6 months ago

r = 1.5 m

F = 12t – 3t2 N

l = 4.5 kgm²

$α = \frac{T}{l} = \frac{\frac{2}{3} (12 t - 3 t^{2})}{4.5} = \frac{1}{3} (12 t - 3 t^{2})$

$\Rightarrow α = 4 t - t^{2}$

$\Rightarrow \frac{d w}{d t} = u t - t^{2} = \int_{0}^{0} d w = \int {(4 t - t^{2})}_{0}^{t} d t$

No. of rev = $\frac{36}{2 π} = \frac{18}{π} = \frac{k}{π} \Rightarrow k = 18$

Upvote

Similar Questions for you

The dimensions of angular impulse is equal to

Alok Kumar Singh

Angular impulse = Change in angular momentum

[J] = [mvr]

[J] = [M¹L²T^–1]

A thin circular ring of mass M and radius R is rotating with a constant angular velocity 2 rads^-1 in a horizontal plane about an axis vertical to its plane and passing through the centre of the ring. If two objects each of mass m be attached gently to the opposite ends of a diameter of ring, the will then rotate with an angular velocity (in rads^-¹).

Raj Pandey

By conservation of Angular momentum

Li = Lf

$M R^{2} ω = (m R^{2} + 2 m R^{2}) ω'$

$\frac{2 M}{M + 2 m} = ω'$

$\Rightarrow$ $ω' = \frac{2 M}{M + 2 m}$

A triangular plate is shown. A force F = 4i - 3j is applied at point P. The torque at point P with respect to point 'O' and 'Q' are :

Vishal Baghel

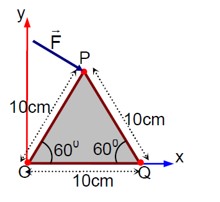
Position vector about O (r_o) = 5i + 5√3j

Force vector (F) = 4i - 3j

Torque about O (τ_o) = r_o × F
τ_o = (5i + 5√3j) × (4i - 3j)
τ_o = -15k - 20√3k = (-15 - 20√3)k

Position vector about Q (r_q) = -5i + 5√3j

Torque about Q (τ_q) = r_q × F
τ_q = (-5i + 5√3j) × (4i - 3j)
τ_q = 15k - 20√3k = (15 - 20√3)k

Consider a 20 kg uniform circular disk of radius 0.2 m. It is pin supported at its centre and is at rest initially. The disk is acted upon by a constant force F = 20 N through a massless string wrapped around its periphery as shown in the figure. Suppose the disk makes n number of revolutions to attain an angular speed of 50 rad s-1. The value of n, to the nearest integer, is ---------.

[Given : In one complete revolution, the disk rotates by 6.28 rad ]

Raj Pandey

Kindly consider the following Image

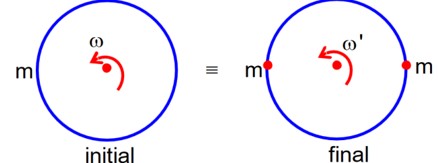
A particle of mass 'm' is moving in time 't' on a trajectory given by r? = 10αt² i? + 5β(t-5) j?. Where α and β are dimensional constants. The angular momentum of the particle become the same as it was for t = 0 at time t = ______ seconds.

Raj Pandey

r? = 10αt²î + 5β (t-5)?
v? = dr? /dt = 20αtî + 5β?
As L? = m (r? × v? )
So, at t=0, L=0
given L is same at t=t as at t=0
⇒ r? × v? = 0
⇒ (10αt²î + 5β (t-5)? ) × (20αtî + 5β? ) = 0
⇒ 50αβt² (î×? ) + 100αβt (t-5) (? ×î) = 0
⇒ 50αβt² k? - 100αβt (t-5) k? = 0
⇒ 50t² - 100t (t-5) = 0
⇒ 50t² - 100t² + 500t = 0
⇒ -