A wheel in uniform motion about an axis passing through its centre and perpendicular to its plane is considered to be in mechanical (translational plus rotational) equilibrium because no net external force or torque is required to sustain its motion. However, the particles that constitute the wheel do experience a centripetal acceleration directed towards the centre. How do you reconcile this fact with the wheel being in equilibrium? How would you set a half-wheel into uniform motion about an axis passing through the centre of mass of the wheel and perpendicular to its plane? Will you require external forces to sustain the motion?

Case – I : When disk slides down

$t_1=\sqrt[]{\frac{2L}{gsin\theta }}..........\left(i\right)$              

Case – II : When disk rolls down

$t_2=\sqrt[]{\frac{2L}{\frac{gsin\theta }{1+{\beta }^2}}}=\sqrt[]{\frac{2L}{\frac{gsin\theta }{1+{\left(\frac{k}{R}\right)}^2}}}=\sqrt[]{\frac{2L}{\frac{gsin\theta }{1+{\left(\frac{R/\sqrt[]{2}}{R}\right)}^2}}}=\sqrt[]{\frac{2L}{\frac{gsin\theta }{1+\frac{1}{2}}}}=\sqrt[]{\frac{4L}{3gsin\theta }}......\left(ii\right)$             

$\Rightarrow \frac{t_1}{t_2}=\sqrt[]{\frac{2L}{gsin\theta }}\times \sqrt[]{\frac{3gsin\theta }{4L}}=\sqrt[]{\frac{3}{2}}$              

This is a multiple choice type question as classified in NCERT Exemplar

a, b, d

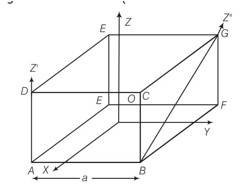
a) according to the perpendicular axes theorem statement 1 is wrong

b) As z’|z so distance between them = a $\frac{\sqrt[]{2}}{2}=\frac{a}{\sqrt[]{2}}$

So according to parallel axes theorem I_z’=I_z+m (a/ $\sqrt[]{2}$ )²= I_z+ma²/2

Hence b is true

c) z’ is not parallel to z hence Pa

This is a multiple choice type question as classified in NCERT Exemplar

b, c

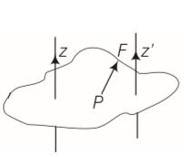
a) When r>r’

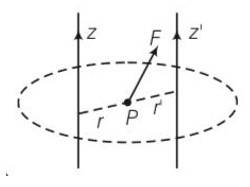
Torque about z-axis t=r $\times$ F

b) t’=r’ $\times F$ which is along negative z axis

c) t_z=Fr = magnitude of torque about z axis where r is perpendicular between F and z axis so torque along positive z axis is greater than negative

This is a multiple choice type question as classified in NCERT Exemplar

a, b, c, d

As we know torque = r $\times$ F = rFsin $\theta$

a) when forces act radially angle =0 hence torque =0

b) when forces are acting on the axis of rotation r=0 torque=0

c) when forces acting parallel to the axis of rotation angle =0 so torq

This is a multiple choice type question as classified in NCERT Exemplar

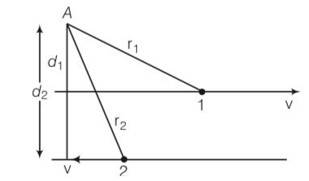
(a), (b)As we know L= r $\times$ p where r is position vector and p is the linear momentum . the direction of L is perpendicular to both r and p by right hand rule.

For particle 1

I₁=r_{1 $\times$} mv is out of the plane of the paper and perpendicu